Définition : Forme linéaire
Soit E un espace vectoriel sur K ( ou
ou  ). Une forme linéaire sur E est une application linéaire de E dans K, K étant considéré comme un espace vectoriel sur lui-même.
). Une forme linéaire sur E est une application linéaire de E dans K, K étant considéré comme un espace vectoriel sur lui-même.
Dans toute cette ressource, le corps de base K des espaces vectoriels considérés est soit le corps des nombres réels soit le corps des nombres complexes.
Il s'agit ici d'une première ressource sur le sujet. Son objectif est de pouvoir être utilisée dans différents contextes.
C'est pourquoi ne sont traitées ici que les propriétés générales et techniques, en particulier dans le cas d'espace vectoriel de type fini. Les propriétés les plus abstraites ne sont donc pas traitées dans cette ressource.
Prérequis indispensables :
Le vocabulaire de base de l'algèbre linéaire et la notion d'espace de type fini (ou dimension finie).
Le calcul matriciel et les formules de changement de base.
Objectifs :
Reconnaître une forme bilinéaire, une forme bilinéaire symétrique, une forme quadratique.
Savoir passer de l'une à l'autre en particulier dans le cas des espaces de type fini.
Savoir écrire la matrice associée à une forme bilinéaire symétrique ou à une forme quadratique dans une base.
Temps de travail prévu : 60 minutes
Pas de prérequis concernant la dualité.
Sommaire :
Dans cette ressource il va être question de formes linéaires, de formes bilinéaires, de formes bilinéaires symétriques, de formes quadratiques. Leurs définitions et propriétés générales vont être développées, ainsi que les liens qui existent entre elles.
Une remarque préliminaire peut être faite : leurs noms comportent tous le mot « forme ». Cela correspond à une propriété qui leur est commune.
Ce sont toutes des applications dont l'espace d'arrivée est K, corps de base des espaces vectoriels qui interviendront.
Dans toute cette ressource le corps de base K des espaces vectoriels considérés est soit le corps des nombres réels soit le corps des nombres complexes.
|
Définition : Forme linéaire Soit E un espace vectoriel sur K ( |
On suppose que E est de dimension p. Soit  une base de E.
une base de E.
|
Caractérisation d'une forme linéaire Soient E un espace vectoriel de dimension p et Une application de E dans K est une forme linéaire sur E si et seulement si il existe p scalaires |
Remarque : l'expression |
Ce résultat pourra être rapproché d'une caractérisation des formes quadratiques sur un espace de type fini.
|
Définition : forme bilinéaire Soient E et F deux espaces vectoriels sur K ( Une forme bilinéaire sur
|
Exemple
Soit F l'espace vectoriel des applications linéaires de E dans K (autrement dit l'espace des formes linéaires).
L'application de  dans K qui à
dans K qui à  associe
associe  est une forme bilinéaire.
est une forme bilinéaire.
Dans toute la suite on va supposer que  .
.
Vocabulaire : Si  , on parle de forme bilinéaire sur E.
, on parle de forme bilinéaire sur E.
Exemples :
Forme bilinéaire sur 
Soit 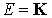 . Soit a un élément de K et f l'application de
. Soit a un élément de K et f l'application de 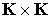 dans K définie par :
dans K définie par :
 .
.
C'est une forme bilinéaire sur K.
Réciproquement toutes les formes bilinéaires sur K sont de ce type. En effet, soit f une forme bilinéaire sur K.
Alors, pour tout  de
de 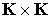 ,
,  (linéarité par rapport à la première variable).
(linéarité par rapport à la première variable).
Or  (linéarité par rapport à la deuxième variable).
(linéarité par rapport à la deuxième variable).
D'où :  .
.
En posant  qui est bien un scalaire, il vient
qui est bien un scalaire, il vient 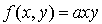 .
.
Soit  et f l'application de
et f l'application de  dans R définie pour tout
dans R définie pour tout  de
de 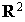 par
par

C'est une forme bilinéaire sur 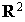 (vérification immédiate).
(vérification immédiate).
|
Définition : forme bilinéaire symétrique Soit E une espace vectoriel sur K.Une forme bilinéaire f sur E est dite symétrique si :
|
Exemples :
Forme bilinéaire symétrique sur 
D'après l'exemple précédent, toute forme bilinéaire sur E est de la forme  . Or il est immédiat que f vérifie
. Or il est immédiat que f vérifie  . Donc toute forme bilinéaire sur K est symétrique.
. Donc toute forme bilinéaire sur K est symétrique.
Soit  . L'application de
. L'application de 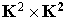 dans K qui à
dans K qui à  associe
associe  est une forme bilinéaire symétrique.
est une forme bilinéaire symétrique.
Soit E l'espace vectoriel des fonctions continues de  dans R. L'application
dans R. L'application  de
de  dans K définie par :
dans K définie par : 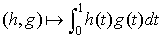 est une forme bilinéaire symétrique sur E.
est une forme bilinéaire symétrique sur E.
Soit f une forme bilinéaire quelconque sur E. Alors il est facile de vérifier que l'application de  dans K définie par :
dans K définie par :  est une forme bilinéaire symétrique.
est une forme bilinéaire symétrique.
Soit  et f l'application de
et f l'application de 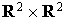 dans R définie pour tout
dans R définie pour tout  de
de 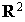 par
par

On a déjà vu au paragraphe précédent que c'est une forme bilinéaire sur 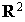 . Ce n'est pas une forme bilinéaire symétrique sur
. Ce n'est pas une forme bilinéaire symétrique sur 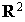 . En effet soit
. En effet soit  . Alors
. Alors  et
et  .
.
|
Définition : forme bilinéaire antisymétrique Soit E une espace vectoriel sur K. Une forme bilinéaire f sur E est dite antisymétrique si :
|
Il est facile de démontrer (cliquez pour voir les détails) que cette propriété est équivalente à

Exemples :
Soit  . L'application de
. L'application de 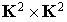 dans K qui à
dans K qui à  associe
associe  est une forme bilinéaire antisymétrique.
est une forme bilinéaire antisymétrique.
Soit E un espace vectoriel de dimension 2 et  une base de E. L'application de
une base de E. L'application de  dans K définie par :
dans K définie par :

est une forme bilinéaire antisymétrique.
Reprenons l'exemple déjà étudié précèdemment.
Soit  et f la forme bilinéaire sur
et f la forme bilinéaire sur 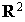 définie pour tout
définie pour tout  de
de 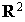 par
par

On a vu que ce n'est pas une forme bilinéaire symétrique. Ce n'est pas non plus une forme bilinéaire antisymétrique sur 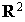 . En effet soit
. En effet soit  . Alors
. Alors 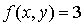 et
et  .
.
Ce dernier exemple montre qu'il y a des formes bilinéaires qui ne sont ni symétriques ni antisymétriques. Il existe cependant un lien de structure fort entre ces différentes notions. Cela fait l'objet du paragraphe suivant.
Soit E un K-espace vectoriel. On note 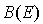 l'ensemble des formes bilinéaires sur E,
l'ensemble des formes bilinéaires sur E,  l'ensemble des formes bilinéaires symétriques sur E et
l'ensemble des formes bilinéaires symétriques sur E et  l'ensemble des formes bilinéaires antisymétriques sur E. On a alors le théorème de structure suivant :
l'ensemble des formes bilinéaires antisymétriques sur E. On a alors le théorème de structure suivant :
|
Théorème : Structure vectorielle de
|
Preuve :
Les propriétés 1) et 2) sont immédiates à démontrer.
Démonstration de la propriété 3)
Soit f une forme bilinéaire quelconque. Supposons qu'il existe une forme bilinéaire symétrique  et une forme bilinéaire antisymétrique
et une forme bilinéaire antisymétrique  telles que
telles que 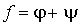 ; cela signifie :
; cela signifie :
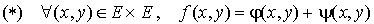 ,
,
d'où 
et donc 
Alors, à partir des relations  et
et  il vient :
il vient :
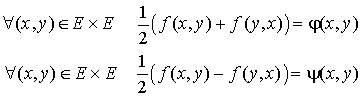
Cela prouve l'unicité de l'écriture d'une forme bilinéaire comme somme d'un élément de  et de
et de  si une telle écriture existe.
si une telle écriture existe.
Pour montrer l'existence d'une telle décomposition, il suffit de vérifier que les applications
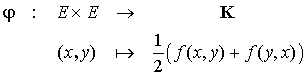
et

conviennent autrement dit que  est une forme bilinéaire symétrique sur E, que
est une forme bilinéaire symétrique sur E, que  est une forme bilinéaire antisymétrique sur E et que
est une forme bilinéaire antisymétrique sur E et que 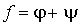 .
.
Toutes ces vérifications sont immédiates, d'où le résultat.
Remarque : bien observer qu'aucune hypothèse concernant la dimension de E n'est nécessaire pour démontrer cette propriété. |
Exemple :
Reprenons l'exemple déjà étudié avec  et f la forme bilinéaire sur
et f la forme bilinéaire sur 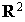 définie pour tout
définie pour tout  de
de 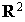 par :
par :

Alors en utilisant les résultats précédents il vient 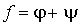 avec
avec

et
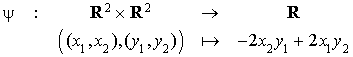
Soit E un espace vectoriel de type fini, et n sa dimension. Soit 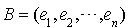 une base de E et f une forme bilinéaire sur E.
une base de E et f une forme bilinéaire sur E.
Soient x et y deux éléments de E que l'on peut écrire de manière unique sous la forme  et
et 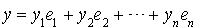 .
.
Alors 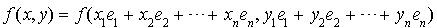 .
.
En utilisant la bilinéarité de f, il vient :

Pour mieux comprendre la construction de cette formule, on peut détailler ce calcul pour  . (Cliquez pour voir ce calcul)
. (Cliquez pour voir ce calcul)
La forme bilinéaire f est donc entièrement définie par les  scalaires
scalaires 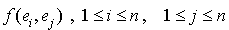 .
.
Réciproquement il est facile de vérifier que toute application de  dans K de la forme
dans K de la forme  est une forme bilinéaire (les notations sont celles indiquées ci-dessus).
est une forme bilinéaire (les notations sont celles indiquées ci-dessus).
Cela permet donc d'énoncer la caractérisation, très utile dans la pratique :
|
Proposition : Caractérisation d'une forme bilinéaire sur un espace de type fini Soit E un espace vectoriel de type fini, et n sa dimension. Soit Une application de
|
Cette propriété peut être interprétée différemment, de manière à obtenir une propriété globale de l'espace vectoriel 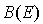 .
.
Introduisons, pour tout couple  avec
avec 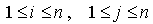 , la forme bilinéaire
, la forme bilinéaire  définie par
définie par 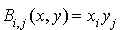 . Alors la formule qui vient d'être trouvée permet d'écrire :
. Alors la formule qui vient d'être trouvée permet d'écrire :

Cela prouve que les formes bilinéaires  engendrent
engendrent 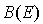 .
.
Or il résulte de la définition des formes bilinéaires  que :
que :

Cela implique (calcul simple) que les formes bilinéaires  sont linéairement indépendantes.
sont linéairement indépendantes.
Ces résultats permettent d'énoncer le théorème :
|
Théorème : Dimension de Soit E un espace vectoriel de type fini, n sa dimension et B une base de E. L'espace vectoriel Plus précisément, les formes bilinéaires |
La forme bilinéaire f est donc entièrement déterminée par les  scalaires
scalaires 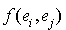 . Cela nous conduit à la définition de la matrice associée à une forme bilinéaire dans une base (page suivante).
. Cela nous conduit à la définition de la matrice associée à une forme bilinéaire dans une base (page suivante).
|
Théorème-définition : Matrice associée à une forme bilinéaire dans une base Soit E un espace vectoriel de type fini, n sa dimension et Soit f une forme bilinéaire sur E. La matrice associée à f dans la base B est la matrice à n lignes et n colonnes dont le terme de la Pour tout L'application de |
Remarque : bien observer la cohérence de l'ordre des indices sur la formule |
Attention : cet isomorphisme n'est pas canonique car il dépend de la base choisie sur E par l'intermédiaire des formes bilinéaires 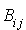 .
.
Exemple :
Reprenons encore l'exemple déjà étudié :
 et f la forme bilinéaire sur
et f la forme bilinéaire sur  définie pour tout
définie pour tout  de
de  par :
par :

On a déjà vu qu'elle n'est ni symétrique ni antisymétrique.
Il s'agit de déterminer la matrice associée à f dans la base canonique, soit A. L'élément de la première ligne première colonne de A est le coefficient de  dans l'expression explicite de
dans l'expression explicite de  ; il est donc égal à 1. De même l'élément de la première ligne deuxième colonne de A est le coefficient de
; il est donc égal à 1. De même l'élément de la première ligne deuxième colonne de A est le coefficient de 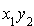 , donc égal à 2. L'élément de la deuxième ligne première colonne de A est le coefficient de
, donc égal à 2. L'élément de la deuxième ligne première colonne de A est le coefficient de  , donc égal à
, donc égal à  . Enfin, l'élément de la deuxième ligne deuxième colonne de A est le coefficient de
. Enfin, l'élément de la deuxième ligne deuxième colonne de A est le coefficient de  , donc égal à
, donc égal à  .
.
 | |
Voir une version animée de cette étape |
| Macromedia Flash - 37,2Ko | ||
La matrice associée à f dans la base canonique est donc  .
.
L'introduction de la matrice associée à une forme bilinéaire permet d'écrire le scalaire  comme un produit de matrices.
comme un produit de matrices.
La convention suivante est utilisée : la matrice scalaire 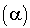 est identifiée au scalaire
est identifiée au scalaire 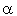 .
.
Soit E un espace vectoriel de type fini, n sa dimension, 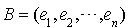 une base de E et f une forme bilinéaire sur E.
une base de E et f une forme bilinéaire sur E.
On a trouvé la formule :

Soit A la matrice associée à f dans la base 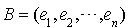 . C'est donc la matrice de
. C'est donc la matrice de 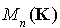 de terme général
de terme général 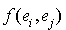 . Soient X et Y les matrices colonnes dont les éléments sont respectivement les coordonnées de x et y dans la base B :
. Soient X et Y les matrices colonnes dont les éléments sont respectivement les coordonnées de x et y dans la base B : 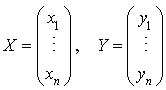 .
.
Alors, en notant  , il vient :
, il vient :  .
.
En notant 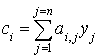 , cela donne :
, cela donne :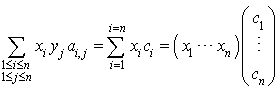 (en utilisant la convention d'identification indiquée ci-dessus).
(en utilisant la convention d'identification indiquée ci-dessus).
La matrice ligne 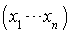 est égale à
est égale à  . Comment interpréter la matrice colonne
. Comment interpréter la matrice colonne  ?
?
Le scalaire 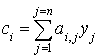 peut être interprété comme le produit
peut être interprété comme le produit  .
.
Donc  et au bilan
et au bilan 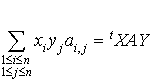 .
.
D'où le résultat.
|
Proposition : Expression matricielle d'une forme bilinéaire Soit E un espace vectoriel de type fini, n sa dimension, Si x et y sont des éléments quelconques de E, X et Y les matrices colonnes dont les éléments sont les coordonnées de x et y respectivement dans la base B, alors on a l'égalité :
|
Remarque : le calcul aurait peut-être paru plus simple si l'on avait démontré cette formule en « partant » de la droite autrement dit si l'on était parti du calcul du produit de matrices |
![]() Changement de base
Changement de base
Bien évidemment la question qui se pose est celle de l'existence d'une formule liant les matrices associées à une forme bilinéaire dans deux bases différentes.
Soient  et
et  deux bases de E, P la matrice de passage de
deux bases de E, P la matrice de passage de  à
à  .
.
Soient x et y deux éléments de E de matrices 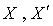 et
et  dans
dans  et
et 
respectivement. Les formules classiques de changement de base donnent les relations : 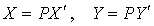 .
.
Alors, si f est une forme bilinéaire sur E, on a
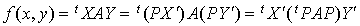 .
.
La formule trouvée prouve que 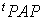 est la matrice associée à f dans la base
est la matrice associée à f dans la base  . On peut donc énoncer la formule de changement de base :
. On peut donc énoncer la formule de changement de base :
|
Proposition : formule de changement de base Soit E un espace vectoriel de type fini, n sa dimension,
|
Attention ! ne pas confondre avec la formule de similitude |
Cette partie est consacrée à l'étude des formes bilinéaires symétriques sur un espace de dimension finie et à la relation existant entre  et l'espace vectoriel des matrices symétriques.
et l'espace vectoriel des matrices symétriques.
Soit E un espace vectoriel de type fini, et n sa dimension. Soit 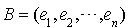 une base de E et f une forme bilinéaire symétrique sur E.
une base de E et f une forme bilinéaire symétrique sur E.
Si  et
et 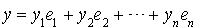 sont deux éléments de E, on a vu que
sont deux éléments de E, on a vu que 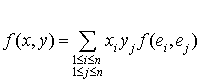 et que la matrice associée à f dans la base B est la matrice de terme général
et que la matrice associée à f dans la base B est la matrice de terme général 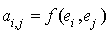 .
.
Or, f est symétrique si et seulement si
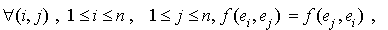
propriété qui équivaut à : 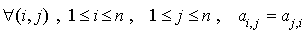 .
.
D'où la proposition.
|
Proposition : caractérisation de la matrice associée dans une base à une forme bilinéaire symétrique Soit E un espace de type fini.
|
Exemple :
Soit  et f la forme bilinéaire symétrique (vérification immédiate) définie pour tout
et f la forme bilinéaire symétrique (vérification immédiate) définie pour tout  de
de 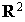 par
par

 | |
Voir une version animée de cette étape |
| Macromedia Flash - 36,4Ko | ||
Alors la matrice associée à f dans la base canonique  de
de 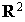 est une matrice de type
est une matrice de type  à coefficients réels égale à :
à coefficients réels égale à :  .
.
Soit 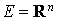 et f la forme bilinéaire symétrique (vérification immédiate) définie pour tout
et f la forme bilinéaire symétrique (vérification immédiate) définie pour tout  de
de  par
par

Alors la matrice associée à f dans la base canonique  de
de  est la matrice unité
est la matrice unité  .
.
![]() Problème réciproque :
Problème réciproque :
Soit E un espace vectoriel de type fini, n sa dimension et 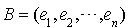 une base de E. Il est clair que la donnée d'une matrice symétrique
une base de E. Il est clair que la donnée d'une matrice symétrique 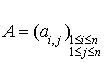 à coefficients dans K permet de construire une forme bilinéaire symétrique f sur E. Il suffit de définir, pour tout i et j compris entre 1 et n,
à coefficients dans K permet de construire une forme bilinéaire symétrique f sur E. Il suffit de définir, pour tout i et j compris entre 1 et n, 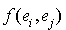 par
par 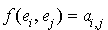 . Elle est bien symétrique puisque pour tout i et j compris entre 1 et n,
. Elle est bien symétrique puisque pour tout i et j compris entre 1 et n,  .
.
Cela nous conduit au théorème suivant
|
Théorème : isomorphisme entre Soit E un K-espace vectoriel de type fini, n sa dimension. Alors l'espace vectoriel |
Preuve :
Ce qui précède prouve l'existence d'une bijection entre ces deux espaces. Il est simple de vérifier que c'est bien une application linéaire.
Attention, cet isomorphisme n'est pas canonique puisqu'il dépend de la base choisie sur E.
![]() Construction de formes bilinéaires symétriques
Construction de formes bilinéaires symétriques
On a même un résultat plus fort puisque cela donne un procédé de construction de forme bilinéaire symétrique à partir d'une matrice symétrique.
Soit 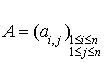 une matrice symétrique à coefficients dans K.
une matrice symétrique à coefficients dans K.
On peut construire un espace vectoriel E, une base  de E et une forme bilinéaire symétrique f telle que A soit la matrice associée à f dans
de E et une forme bilinéaire symétrique f telle que A soit la matrice associée à f dans  .
.
Pour cela on prend 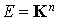 ,
,  la base canonique de
la base canonique de  et on définit f par
et on définit f par 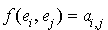 .
.
Exemple :
Soit la matrice  . C'est une matrice symétrique.
. C'est une matrice symétrique.
 | |
Voir une version animée de cette étape |
| Macromedia Flash - 47,8Ko | ||
Alors l'application f de  dans R définie pour tout
dans R définie pour tout 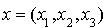 et tout
et tout 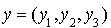 par
par 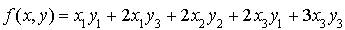 est une forme bilinéaire symétrique sur
est une forme bilinéaire symétrique sur  admettant A comme matrice associée dans la base canonique.
admettant A comme matrice associée dans la base canonique.
En appliquant le résultat général vu pour les formes bilinéaires au cas des formes bilinéaires symétriques, et en utilisant toujours la même convention (la matrice scalaire 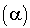 est identifiée au scalaire
est identifiée au scalaire 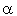 ), il vient :
), il vient :
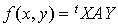 avec A symétrique.
avec A symétrique.
où  , et
, et 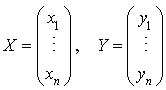
Remarque : Comme
Cela pouvait aussi être justifié en utilisant la symétrie de f. |
![]() Changement de base
Changement de base
La formule de changement de base, vue pour une forme bilinéaire quelconque, est évidemment encore valable si la forme est symétrique.
On peut d'ailleurs observer directement que si A est une matrice symétrique, la matrice 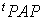 est aussi symétrique.
est aussi symétrique.
Dans cette partie est introduite une nouvelle notion celle de forme quadratique. Elle est tout d'abord étudiée dans le cas d'espace vectoriel quelconque puis dans celui d'un espace de type fini.
|
Définition : « Forme quadratique associée à une forme bilinéaire symétrique ». Soit E un espace vectoriel sur K ( La « forme quadratique associée à la forme bilinéaire symétrique f » est l'application
|
Remarque : dans cette définition, l'expression « Forme quadratique associée à une forme bilinéaire symétrique » est considérée comme un seul mot. |
Exemples : reprenons les exemples de formes bilinéaires symétriques
Soit 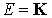 , a un élément de K et f la forme bilinéaire symétrique sur K définie par
, a un élément de K et f la forme bilinéaire symétrique sur K définie par
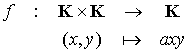
Alors
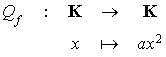
Soit  et h la forme bilinéaire symétrique sur
et h la forme bilinéaire symétrique sur 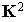 dans K définie par
dans K définie par

Alors

Soit E l'espace vectoriel des fonctions continues de  dans R et
dans R et  la forme bilinéaire symétrique sur E définie par :
la forme bilinéaire symétrique sur E définie par :
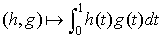
Alors 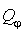 est l'application de E dans R définie par :
est l'application de E dans R définie par :
 .
.
|
Proposition : Quelques propriétés immédiates Soit E un espace vectoriel sur K (
|
Preuve : Les démonstrations sont simples
Soit x un élément quelconque de E et  un scalaire quelconque. Alors
un scalaire quelconque. Alors  .
.
Soit  appartenant à
appartenant à  . Alors en utilisant la bilinéarité de f il vient :
. Alors en utilisant la bilinéarité de f il vient :

Comme f est symétrique cela donne

D'où le résultat.
Ces propriétés sont des conditions nécessaires pour qu'une application q de E dans K soit la forme quadratique associée à une forme bilinéaire symétrique f donnée.
En fait, on va définir la notion de forme quadratique « tout court » naturellement à partir de la définition précédente et montrer que les conditions nécessaires ci-dessus sont aussi des conditions suffisantes.
|
Définition d'une forme quadratique Une application q de E dans K est une forme quadratique sur E si il existe une forme bilinéaire symétrique f sur E telle que, pour tout x de E, |
Evidemment c'est une définition très simple mais qui n'est pas très commode dans la pratique, même si parfois l'expression de f saute aux yeux.
Le théorème suivant permet d'avoir une caractérisation des formes quadratiques plus utilisable.
|
Théorème : caractérisation des formes quadratiques Une application Q de E dans K est une forme quadratique sur E si et seulement si les deux propriétés suivantes sont satisfaites :
Si ces conditions sont satisfaites, Q est la forme quadratique associée à f et la forme bilinéaire symétrique f est souvent appelée forme polaire associée à Q. |
Il est clair que si les propriétés i) et ii) sont satisfaites, on a :

et donc Q est la forme quadratique associée à f.
Remarque : Pour démontrer qu'une application q d'un espace vectoriel quelconque (c'est-à-dire non nécessairement de type fini) dans son corps de base est une forme quadratique, on a à priori deux méthodes : « deviner » une forme bilinéaire symétrique f telle que Cependant, la propriété i) est souvent utilisée pour démontrer qu'une application q n'est pas une forme quadratique. |
Commentaire sur le choix fait pour la définition d'une forme quadratique Nous avons fait le choix de définir les formes quadratiques à partir des formes bilinéaires symétriques. On trouve chez certains auteurs une définition des formes quadratiques simplement à partir des formes bilinéaires. La définition est alors la suivante : une application q de E dans K est une forme quadratique s'il existe une forme bilinéaire (quelconque) Il nous est apparu inutile d'introduire cette étape supplémentaire qui n'a aucun rôle dans la suite de l'étude. |
Dans le cas d'une forme quadratique sur un espace de type fini on a une caractérisation beaucoup plus simple qui est utilisée systématiquement. C'est l'objet du paragraphe suivant.
Soit E un espace vectoriel de type fini, n sa dimension, 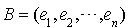 une base de E et f une forme bilinéaire symétrique sur E. Soit A la matrice associée à f dans la base B. C'est une matrice symétrique.
une base de E et f une forme bilinéaire symétrique sur E. Soit A la matrice associée à f dans la base B. C'est une matrice symétrique.
Si  sont des éléments quelconques de E, et si X et Y sont les matrices colonnes dont les éléments sont les coordonnées de x et y respectivement dans la base B, alors
sont des éléments quelconques de E, et si X et Y sont les matrices colonnes dont les éléments sont les coordonnées de x et y respectivement dans la base B, alors 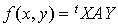 . Il s'en déduit immédiatement que :
. Il s'en déduit immédiatement que :
 .
.
Si l'on développe ce produit matriciel, il vient

Introduisons la définition suivante :
|
Définition : expression polynomiale homogène de degré 2 Soit t une application de E dans K pour laquelle il existe
On dit que |
Il résulte de la formule 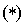 que
que 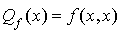 est une expression polynomiale homogène de degré 2 par rapport aux coordonnées de x dans la base B de E.
est une expression polynomiale homogène de degré 2 par rapport aux coordonnées de x dans la base B de E.
Réciproquement si l'on a une expression polynomiale homogène de degré 2 par rapport aux coordonnées de x dans la base B de E, c'est une forme quadratique sur E.
En effet, soit q une application de E dans K pour laquelle il existe  éléments de K,
éléments de K,  tels que q soit l'application définie par :
tels que q soit l'application définie par :
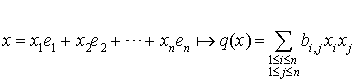
On peut écrire autrement cette expression en mettant en évidence les termes « carrés » c'est à dire de la forme  et les termes « rectangles » c'est-à-dire de la forme
et les termes « rectangles » c'est-à-dire de la forme 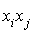 avec
avec  . Le coefficient du terme
. Le coefficient du terme  est
est  ; celui du terme
; celui du terme 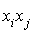 est
est  , enfin celui du terme
, enfin celui du terme  est
est  . Bien évidemment on peut regrouper ces deux derniers termes, ce qui permet d'écrire :
. Bien évidemment on peut regrouper ces deux derniers termes, ce qui permet d'écrire :
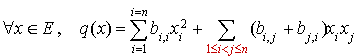
Soient les scalaires  définis pour tout couple
définis pour tout couple  appartenant à
appartenant à  par
par  .
.
Ils vérifient en particulier les relations

Alors, il vient que
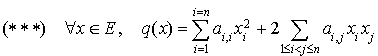
Deux façons de terminer la démonstration.
Méthode matricielle.
Cette formule peut être écrite matriciellement sous la forme :

où A est la matrice de terme général  .
.
La démonstration est du même type que celle faite pour trouver l'expression matricielle d'une forme bilinéaire symétrique. Cliquez pour voir les détails.
Alors si f est la forme bilinéaire symétrique sur E dont la matrice associée dans la base B est égale à A, q est la forme quadratique associée à f.
Vocabulaire :
On dit indifféremment que A est la matrice associée à f ou la matrice associée à q dans la base B.
Méthode utilisant la caractérisation d'une forme quadratique.
Il suffit de vérifier à partir de l'expression  (les calculs à faire sont simples) que l'application q vérifie les deux conditions :
(les calculs à faire sont simples) que l'application q vérifie les deux conditions :

L'application f définie par  est bilinéaire symétrique.
est bilinéaire symétrique.
D'où la propriété suivante :
|
Proposition : Caractérisation d'une forme quadratique sur un espace de type fini. Soit E un espace vectoriel de type fini. |
Dans la pratique, lorsque E est un espace de type fini, cela donne un procédé extrêmement commode pour reconnaître si une application de E dans K est une forme quadratique.
Ces résultats permettent d'énoncer le théorème fondamental suivant, valable dans un espace vectoriel quelconque.
|
Théorème : Isomorphisme entre Soit E un espace vectoriel sur K. Soient
|
Cas d'un espace de type fini
Soit E un espace de dimension n et 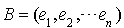 une base de E. On a vu que si q est une forme quadratique, il existe des scalaires
une base de E. On a vu que si q est une forme quadratique, il existe des scalaires 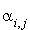 tels que pour tout i et j compris entre 1 et n,
tels que pour tout i et j compris entre 1 et n,  et tels que :
et tels que :

Notons  et
et  les formes quadratiques
les formes quadratiques  et
et 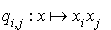 . La propriété
. La propriété 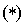 équivaut à :
équivaut à :
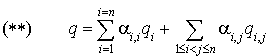
la propriété  prouve que les formes
prouve que les formes  et
et  forment une famille génératrice de
forment une famille génératrice de 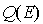 . Il est immédiat de vérifier qu'elles sont linéairement indépendantes. Elles définissent donc une base de
. Il est immédiat de vérifier qu'elles sont linéairement indépendantes. Elles définissent donc une base de 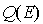 . Cela prouve que
. Cela prouve que 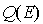 est de type fini.
est de type fini.
La base trouvée est extrêmement utile pour déterminer simplement la forme polaire associée à une forme quadratique donnée (dans l'autre sens si on connaît la forme bilinéaire symétrique, trouver la forme quadratique associée est immédiat, il suffit d'écrire  ).
).
En effet, à cause de l'isomorphisme indiqué dans le théorème, si f est la forme polaire associée à q,  celle associée à
celle associée à  et si
et si  ,
, 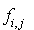 celle associée à
celle associée à  , il vient :
, il vient :

et les formes bilinéaires symétriques  et
et 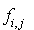 définissent une base de
définissent une base de  . Il ne reste donc qu'à les déterminer.
. Il ne reste donc qu'à les déterminer.
En utilisant la définition, il vient  et
et 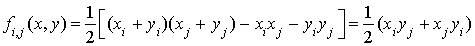 .
.
D'où la proposition :
|
Proposition : base de Soit E un espace de dimension n,
et
Ces formes bilinéaires symétriques |
Ce qui donne le corollaire pratique suivant :
|
Corollaire : Expression explicite de la forme polaire d'une forme quadratique Soit E un espace de dimension n et
|
Ce résultat est constamment utilisé dans la pratique.
Exemple : Soit  .
.
Soit q l'application de E dans R définie pour tout 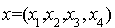 par
par 
 | |
Voir une version animée de ces étapes |
| Macromedia Flash - 67,0Ko | ||
Comme  est une expression polynômiale homogène de degré 2 par rapport aux coordonnées
est une expression polynômiale homogène de degré 2 par rapport aux coordonnées  de x dans la base canonique, c'est une forme quadratique et sa forme polaire est définie pour tout
de x dans la base canonique, c'est une forme quadratique et sa forme polaire est définie pour tout 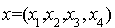 et
et 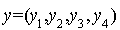 de
de 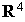 par
par  .
.
La matrice associée à f (ou à q) dans la base canonique de  est :
est :
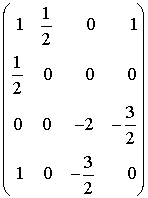 .
.
La connaissance d'une base explicite permet de déterminer la dimension de 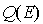 et de
et de  .
.
|
Proposition : dimension de Soit E un espace de dimension n. Alors
|
Preuve de la formule :
Pour trouver la dimension de l'espace vectoriel des formes quadratiques il suffit de compter les éléments de la base trouvée donc le nombre de formes  où i est un entier compris entre 1 et n et de formes
où i est un entier compris entre 1 et n et de formes  avec
avec 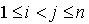 . Il y a exactement n formes
. Il y a exactement n formes  et
et  (autant que de façons de prendre deux éléments distincts i et j parmi n éléments) formes
(autant que de façons de prendre deux éléments distincts i et j parmi n éléments) formes  . Comme
. Comme 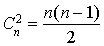 , on a
, on a 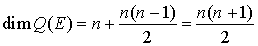 .
.