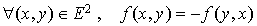

Démonstration de l'équivalence
Il s'agit donc de démontrer que, si f est une forme bilinéaire, les propriétés suivantes sont équivalentes :
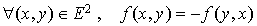

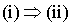 :
:
Soit x un élément quelconque de E. En appliquant (i) au couple 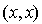 on obtient
on obtient 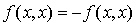 .
.
Comme le corps de base est R ou C, cela entraîne 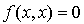 .
.
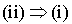
Soient x et y deux éléments de E. Considérons 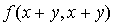 .
.
D'une part en utilisant la propriété (ii), on obtient 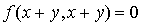 .
.
D'autre part, en utilisant l'hypothèse f bilinéaire on peut développer 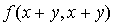 et on obtient :
et on obtient :
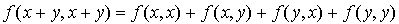 .
.
Or en utilisant (ii) il vient 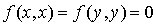 .
.
Donc ces calculs conduisent à l'égalité : 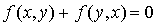 .
.
D'où le résultat.