Définition 1 : famille orthogonale
Une famille de p vecteurs 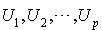 est orthogonale si pour tout couple
est orthogonale si pour tout couple 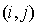 où i et j sont deux éléments distincts de
où i et j sont deux éléments distincts de 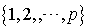 , les vecteurs
, les vecteurs 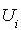 et
et 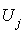 sont orthogonaux, c'est-à-dire tels que
sont orthogonaux, c'est-à-dire tels que 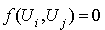
Ce cours comporte deux grands thèmes : le premier concerne les bases orthogonales ou orthonormales par rapport à une forme quadratique (respectivement par rapport à une forme bilinéaire symétrique).
Le second a pour finalité l'algorithme de Gauss qui permet de décomposer une forme quadratique en combinaison linéaire de carrés de formes linéaires linéairement indépendantes. Cette partie est achevée par le théorème d'inertie de Sylvester.
Prérequis indispensables :
Les généralités sur les formes bilinéaires symétriques et les formes quadratiques.
Le calcul matriciel et les formules de changement de base.
Prérequis utiles :
Quelques notions sur le dual d'un espace vectoriel et la notion de base duale. Cependant toutes les propriétés nécessaires sont rappelées au fur et à mesure des besoins. Un étudiant ne connaissant pas la théorie de la dualité peut donc tout de même étudier cette ressource en particulier l'algorithme de Gauss.
Objectifs :
Décomposer une forme quadratique en carrés et déterminer à partir de là sa signature, son rang. Savoir dire à partir de là si une forme quadratique est ou non dégénérée, et éventuellement utiliser une telle décomposition pour déterminer les vecteurs isotropes.
Caractériser et trouver explicitement une base orthogonale relativement à une forme quadratique ou à une forme bilinéaire symétrique.
Temps de travail prévu : 105 minutes
Comptez environ 90 minutes pour le cours et 15 minutes pour le QCI.
Les étudiants non intéressés par l'aspect théorique de ces notions peuvent aller directement à l'algorithme de Gauss et ses exemples et admettre le théorème de Sylvester qui leur permet d'avoir toutes les applications qui leur seront nécessaires.
Lorsque l'on étudie les formes bilinéaires symétriques ou les formes quadratiques sur un espace de type fini, la matrice qu'on leur associe par rapport à une base de l'espace considéré joue un rôle pratique important. Il est clair que plus cette matrice est « simple » c'est-à-dire comporte beaucoup de zéros et plus les calculs sont faciles. Evidemment les matrices les plus simples en ce sens sont les matrices diagonales.
L'objet de cette ressource est de caractériser et d'étudier l'existence de bases dans lesquelles la matrice associée à une forme quadratique (respectivement à une forme bilinéaire symétrique) est diagonale, et de donner, s'il y a lieu, un algorithme pour déterminer explicitement de telles bases.
Dans toute cette ressource les espaces vectoriels considérés sont des espaces vectoriels de type fini sur le corps de nombres réels ou sur le corps des nombres complexes.
Soit E un espace vectoriel de dimension n. Soit f une forme bilinéaire symétrique sur E, q la forme quadratique associée.
|
Définition 1 : famille orthogonale Une famille de p vecteurs |
|
Définition 2 : famille orthonormale Une famille de p vecteurs
|
On a immédiatement la propriété suivante :
|
Propriété des familles orthonormales : Une famille orthonormale de p vecteurs |
La preuve de cette propriété est simple :
Soit 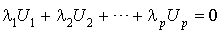 une combinaison linéaire nulle des vecteurs
une combinaison linéaire nulle des vecteurs 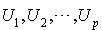 .
.
Soit k un entier quelconque compris entre 1 et p.
Alors 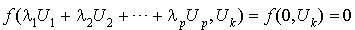 .
.
Comme f est bilinéaire cela donne 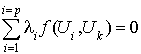 . Comme la famille est orthonormale,
. Comme la famille est orthonormale,
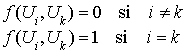
et donc le seule terme de la somme qui reste est 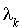 . Il s'en déduit l'égalité :
. Il s'en déduit l'égalité :
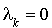 .
.
Ceci achève la démonstration.
|
Remarque : Ce résultat n'est pas vrai en général pour une famille orthogonale. Considérons pour s'en convaincre l'exemple suivant : soit |
La problématique de départ est de trouver une caractérisation des bases de E telles que la matrice associée à f (ou à q) par rapport à l'une de ces bases soit diagonale.
Si 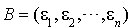 est une telle base de E. La matrice associée à f (ou à q) par rapport à cette base est diagonale, c'est-à-dire de la forme :
est une telle base de E. La matrice associée à f (ou à q) par rapport à cette base est diagonale, c'est-à-dire de la forme :
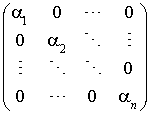
où les 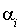 sont des éléments de K dont certains peuvent être nuls.
sont des éléments de K dont certains peuvent être nuls.
On a alors :
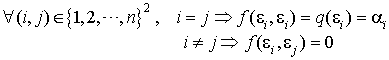
Cela conduit à la définition de la notion de base orthogonale.
|
Définitions : base orthogonale, base orthonormale relativement à une forme bilinéaire symétrique On dit qu'une base
On dit qu'une base |
|
Remarques :
|
Conséquence : on a bien une réponse à la question posée.
Une base est orthogonale relativement à une forme bilinéaire symétrique f si et seulement si la matrice associée à f par rapport à cette base est une matrice diagonale, les termes de la diagonale principale pouvant être nuls ou non.
Une base est orthonormale relativement à une forme bilinéaire symétrique f si et seulement si la matrice associée à f par rapport à cette base est la matrice unité.
Notation :
La notion de base orthonormale ou orthogonale est relative à la forme quadratique ou bilinéaire symétrique considérée. C'est pourquoi lorsqu'il y a un risque de confusion, on utilise le vocabulaire suivant : base f-orthogonale ou base q-orthogonale
Exemples :
Soit 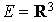 et
et 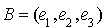 sa base canonique.
sa base canonique.
Soit l'application q de 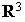 dans R définie pour tout
dans R définie pour tout 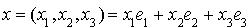 de
de 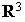 par :
par :
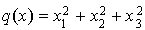 .
.
Alors la matrice associée à q dans la base canonique est la matrice unité d'ordre 3 et la forme bilinéaire symétrique qui lui est associée (théorème précédent) est définie pour tout élément 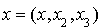 et
et 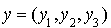 par :
par :
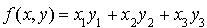 .
.
On reconnaît le produit scalaire euclidien de la géométrie classique, la quantité 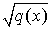 étant la norme euclidienne du vecteur x.
étant la norme euclidienne du vecteur x.
La base canonique de 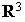 est donc une base orthonormale pour f. On retrouve la situation classique de la géométrie euclidienne de l'espace.
est donc une base orthonormale pour f. On retrouve la situation classique de la géométrie euclidienne de l'espace.
Soit 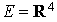 et
et 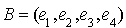 sa base canonique.
sa base canonique.
Soit l'application 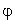 de
de 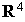 dans R définie pour tout
dans R définie pour tout 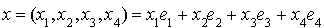 de
de 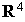 par :
par :
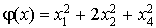 .
.
Alors la matrice associée à 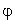 dans la base canonique est la matrice
dans la base canonique est la matrice 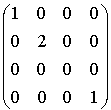 .
.
La base canonique est donc une base orthogonale pour 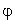 ou est
ou est 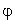 -orthogonale
-orthogonale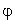 -orthonormale
-orthonormale
La première question qui se pose est celle de l'existence de telles bases.
La réponse est positive pour l'existence d'une base orthogonale, mais il faut des conditions supplémentaires pour l'existence d'une base orthonormale.
|
Théorème : Existence d'une base orthogonale relativement à une forme bilinéaire symétrique (ou à une forme quadratique) Soit E un K-espace vectoriel de dimension n et f une forme bilinéaire symétrique non nulle de rang r (r est donc strictement positif). Alors il existe une base
|
Conséquence immédiate :
La matrice associée à f dans une telle base est de la forme :
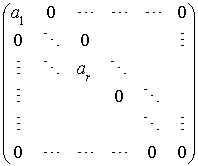 si r est strictement inférieur à n,
si r est strictement inférieur à n,
ou : 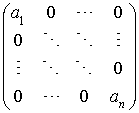 si
si 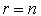 , les
, les 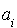 étant des scalaires non nuls.
étant des scalaires non nuls.
|
Corollaire Si |
Autrement dit, déterminer explicitement une base orthogonale relativement à f et déterminer la matrice associée à f dans cette base permet de trouver explicitement le rang d'une forme bilinéaire symétrique.
Preuve du théorème :
On procède par récurrence sur la dimension de E.
Pour 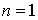 , il n'y a rien à dire.
, il n'y a rien à dire.
Supposons la propriété vraie pour tout espace de dimension 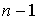 .
.
Démontrons la pour un espace de dimension n.
Soit 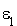 un vecteur tel que
un vecteur tel que 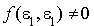 ; (un tel vecteur existe puisque f étant non nulle, la forme quadratique associée est non nulle).
; (un tel vecteur existe puisque f étant non nulle, la forme quadratique associée est non nulle).
Considérons la forme linéaire définie sur E par
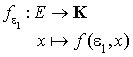
C'est une forme linéaire non nulle donc elle est surjective, son rang est égal à 1 et par conséquent d'après le théorème du rang, son noyau est de dimension 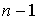 . Donc
. Donc 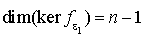 . De plus comme
. De plus comme 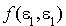 est non nul, le vecteur
est non nul, le vecteur 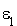 n'appartient pas à
n'appartient pas à 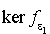 et donc
et donc 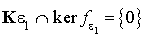 .
.
On déduit de ces deux résultats l'égalité 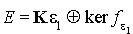 .
.
Il est clair que la restriction à 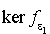 de la forme bilinéaire symétrique f est une forme bilinéaire symétrique sur
de la forme bilinéaire symétrique f est une forme bilinéaire symétrique sur 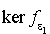 . On peut donc appliquer l'hypothèse de récurrence.
. On peut donc appliquer l'hypothèse de récurrence.
Il existe donc une base 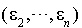 de
de 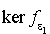 orthogonale pour la restriction de f à
orthogonale pour la restriction de f à 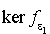 . Il est évident que ces vecteurs sont orthogonaux pour f.
. Il est évident que ces vecteurs sont orthogonaux pour f.
En résumé :
comme 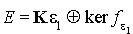 ,
, 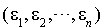 est une base de E
est une base de E
d'après la définition de 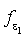 , pour tout i,
, pour tout i, 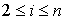 ,
, 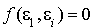 et donc le vecteur
et donc le vecteur 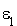 est orthogonal à tous les vecteurs
est orthogonal à tous les vecteurs 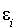 , pour i compris entre 2 et n.
, pour i compris entre 2 et n.
d'après les propriétés des vecteurs 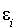 , pour i compris entre 2 et n on a :
, pour i compris entre 2 et n on a :
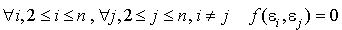
L'ensemble de ces propriétés prouve que 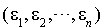 est une base f-orthogonale de E.
est une base f-orthogonale de E.
La matrice associée à f dans cette base est une matrice diagonale de rang r, le rang de la forme bilinéaire symétrique. Ce rang est égal au nombre de scalaires non nuls sur la diagonale principale. Quitte à renuméroter les vecteurs on peut supposer que ce sont les r premiers et on a donc le résultat.
Pour illustrer cette dernière phrase on peut reprendre l'exemple (2) vu ci-dessus. La base canonique 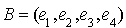 est une base orthogonale pour la forme quadratique
est une base orthogonale pour la forme quadratique 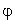 considérée et la matrice associée à
considérée et la matrice associée à 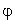 dans cette base est
dans cette base est 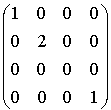 . Alors la base
. Alors la base 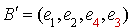 est une base
est une base 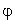 -orthogonale satisfaisant aux conditions du théorème.
-orthogonale satisfaisant aux conditions du théorème.
Interprétation des vecteurs 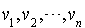 lorsque
lorsque 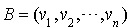 est une base f-orthogonale satisfaisant aux conditions du théorème
est une base f-orthogonale satisfaisant aux conditions du théorème
On suppose f de rang strictement inférieur à n. Soit 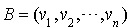 une base orthogonale de E telle que :
une base orthogonale de E telle que :
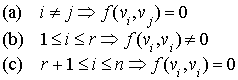
alors, 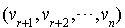 est une base de
est une base de 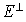 (orthogonal de E relativement à la forme bilinéaire symétrique f).
(orthogonal de E relativement à la forme bilinéaire symétrique f).
![]() Pour voir la preuve de ce résultat, cliquez.
Pour voir la preuve de ce résultat, cliquez.
On peut donner une traduction matricielle du théorème.
|
Proposition : Traduction matricielle Soit A une matrice carrée symétrique à coefficients dans K (avec |
Cela résulte, d'une part de l'isomorphisme entre espace vectoriel des matrices symétriques et espace vectoriel des formes bilinéaires symétriques, et d'autre part, de la formule de changement de base pour les matrices associées à une forme bilinéaire symétrique.
Attention
: ce théorème ne prouve pas que la matrice A est diagonalisable. En effet, en général, la matrice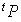 est différente de la matrice
est différente de la matrice 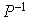 .
.
Le problème de la diagonalisation des matrices symétriques réelles est étudié dans le cadre des espaces euclidiens.
![]() Problème des bases orthonormales
Problème des bases orthonormales
Le problème de l'existence d'une base orthonormale est moins simple.
Une condition nécessaire d'existence d'une base orthonormale pour une forme bilinéaire symétrique f est que f soit de rang n.
En effet toutes les matrices associées à une forme bilinéaire symétrique ont le même rang. Or s'il existe une base orthonormale, la matrice associée à f dans cette base est 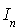 qui est de rang n.
qui est de rang n.
Mais cette condition n'est pas suffisante. Pour s'en convaincre on va étudier l'exemple suivant : soit q la forme quadratique définie sur 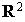 par
par 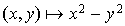 . La matrice qui lui est associée dans la base canonique est
. La matrice qui lui est associée dans la base canonique est 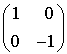 . S'il existe une base orthonormale, il existe une matrice inversible P telle que
. S'il existe une base orthonormale, il existe une matrice inversible P telle que 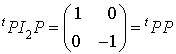 .
.
Si 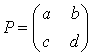 , alors
, alors 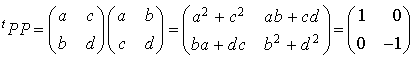 .
.
Ceci implique, entre autres, l'égalité 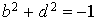 ce qui est absurde dans R. Il n'existe donc pas de base orthonormale relativement à q.
ce qui est absurde dans R. Il n'existe donc pas de base orthonormale relativement à q.
On peut donner cependant un exemple où l'on sait construire une base orthonormale à partir d'une base orthogonale pour une forme quadratique de rang n. Il s'agit des formes quadratiques de rang n sur un espace de dimension n sur le corps des nombres complexes
.En effet si q est une telle forme et 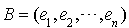 est une base orthogonale relative à q,
est une base orthogonale relative à q,
on a 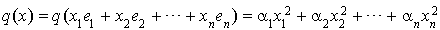 où les
où les 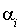 sont des nombres complexes non nuls.
sont des nombres complexes non nuls.
Soit 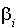 des nombres complexes tels que, pour tout i compris entre 1 et n,
des nombres complexes tels que, pour tout i compris entre 1 et n, 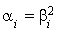 et les vecteurs
et les vecteurs 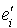 définis, pour tout i compris entre 1 et n, par
définis, pour tout i compris entre 1 et n, par 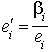 . Alors
. Alors 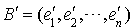 est une base (les nombres complexes
est une base (les nombres complexes 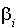 sont non nuls) et elle est orthonormale relativement à q puisque
sont non nuls) et elle est orthonormale relativement à q puisque 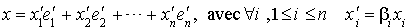 et donc
et donc 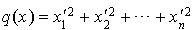 .
.
D'où la propriété :
|
Proposition : Existence de base orthonormale relativement à une forme quadratique sur un espace vectoriel sur le corps des nombres complexes C Soit E un C-espace vectoriel de dimension n et q une forme quadratique sur E. Une condition nécessaire et suffisante pour qu'il existe une base q-orthonormale est que q soit de rang n. |
On a de manière immédiate un résultat très utile sur la matrice de passage d'une base orthonormale à une autre base orthonormale.
|
Proposition : matrice de passage d'une base orthonormale à une autre base orthonormale Soit f une forme bilinéaire symétrique sur un espace vectoriel de type fini, telle qu'il existe au moins une base f-orthonormale. Alors la matrice P de passage d'une base f-orthonormale à une autre base f-orthonormale vérifie la relation |
Preuve :
La matrice associée à une forme bilinéaire symétrique par rapport à une base orthonormale est la matrice unité d'ordre n. Si on a deux bases orthonormales, la formule de changement de base donne donc : 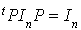 et donc
et donc 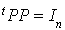 .
.
La démonstration du théorème d'existence d'une base orthogonale qui vient d'être faite est simple en ce sens qu'elle ne met pas en œuvre des propriétés mathématiques complexes. Elle donne le résultat théorique mais n'est pas effective, c'est-à-dire ne permet pas de trouver effectivement une base orthogonale.
L'algorithme de Gauss qui va être étudié redonne une démonstration de l'existence d'une telle base et permet à la fois d'en construire une effective et de connaître sans calculs supplémentaires la matrice associée à la forme bilinéaire symétrique dans cette base.
Soit q une forme quadratique sur un espace vectoriel de dimension n. Le théorème démontré dans le paragraphe précédent assure l'existence d'une base orthogonale pour q. Si 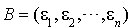 est une telle base, il existe des scalaires
est une telle base, il existe des scalaires 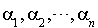 (certains pouvant être nuls) tels que si un élément x de E est écrit sous la forme
(certains pouvant être nuls) tels que si un élément x de E est écrit sous la forme 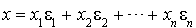 , alors
, alors 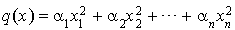 .
.
On considère dans le dual de E, la base 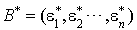 base duale de la base B. Le scalaire
base duale de la base B. Le scalaire 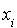 est l'image de x par la forme linéaire
est l'image de x par la forme linéaire 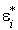 . Alors on a la formule :
. Alors on a la formule :
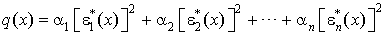
Cela signifie que l'on a écrit q comme combinaison linéaire de carrés de formes linéaires linéairement indépendantes.
![]() Rappel sur la notion de base duale
Rappel sur la notion de base duale
Réciproquement, supposons qu'il existe des formes linéaires 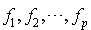 , linéairement indépendantes, telles que
, linéairement indépendantes, telles que 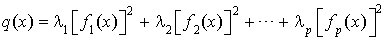 , où les
, où les 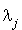 sont non nuls.
sont non nuls.
Si p est strictement inférieur à n, il existe, d'après le théorème de la base incomplète, des formes linéaires 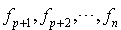 telles que
telles que 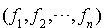 soit une base de
soit une base de 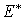 . Si p est égal à n on a directement une base de
. Si p est égal à n on a directement une base de 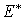 . Ce qui suit est donc commun aux deux cas.
. Ce qui suit est donc commun aux deux cas.
Soit 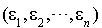 la base de E antéduale de la base
la base de E antéduale de la base 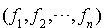 c'est-à-dire telle que
c'est-à-dire telle que 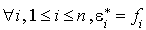 . Cela signifie donc que :
. Cela signifie donc que :
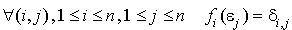
où 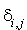 désigne le symbole de Kronecker.
désigne le symbole de Kronecker.
Alors si 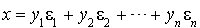 ,
, 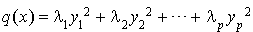 , ce qui prouve que la base
, ce qui prouve que la base 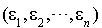 est une base orthogonale pour q et que la matrice associée à q dans la base
est une base orthogonale pour q et que la matrice associée à q dans la base 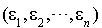 est :
est :
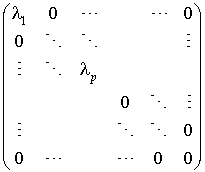 si p est strictement inférieur à n,
si p est strictement inférieur à n,
ou : 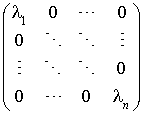 si p est égal à n.
si p est égal à n.
On en déduit aussi que p est le rang de q.
|
Conclusion : Trouver une base orthogonale relativement à q revient à décomposer q en combinaison linéaire de carrés de formes linéaires linéairement indépendantes. |
|
Remarque : Souvent, dans la pratique on dit « décomposer la forme quadratique en carrés » ce qui est incorrect car incomplet mais beaucoup plus rapide. |
Les notations précédentes sont conservées.
Connaissant n formes linéaires, linéairement indépendantes 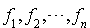 , il s'agit de chercher explicitement une base
, il s'agit de chercher explicitement une base 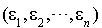 vérifiant les conditions :
vérifiant les conditions :
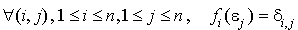
On va donner deux méthodes.
Première méthode :
Soit j un entier compris entre 1 et n. Le vecteur 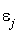 satisfait aux n relations :
satisfait aux n relations :
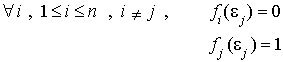
Soit 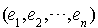 une base de E et
une base de E et 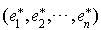 sa base duale. Alors en exprimant
sa base duale. Alors en exprimant 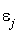 sur la base
sur la base 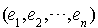 et les formes
et les formes 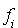 sur la base
sur la base 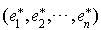 , les conditions précédentes se traduisent par un système de n équations à n inconnues qui sont les coordonnées de
, les conditions précédentes se traduisent par un système de n équations à n inconnues qui sont les coordonnées de 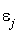 sur
sur 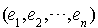 .
.
Donc on trouve la base 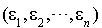 en résolvant n systèmes de n équations à n inconnues.
en résolvant n systèmes de n équations à n inconnues.
En fait les premiers membres de ces systèmes sont les mêmes, seuls changent les deuxièmes membres. Par conséquent, dans la pratique, il suffit d'utiliser une fois la méthode du Pivot de Gauss avec un second membre quelconque puis de trouver les solutions en prenant successivement tous les seconds membres adéquats. L'exemple qui va être donné illustrera bien l'algorithme.
Deuxième méthode :
Elle consiste à trouver une formule traduisant le procédé précédent.
Les formes 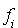 étant données par la décompositions en carrés, on connaît la matrice R de passage de la base
étant données par la décompositions en carrés, on connaît la matrice R de passage de la base 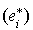 à la base
à la base 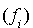 . Pour déterminer les vecteurs
. Pour déterminer les vecteurs 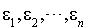 tels que
tels que 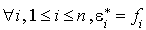 , il suffit de connaître l'expression de chacun d'eux dans la base
, il suffit de connaître l'expression de chacun d'eux dans la base 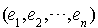 . Autrement dit il s'agit de déterminer la matrice de passage P de la base
. Autrement dit il s'agit de déterminer la matrice de passage P de la base 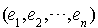 à la base
à la base 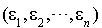 .
.
Or P est la matrice de l'application identique de E en choisissant 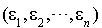 comme base de E espace de départ, et
comme base de E espace de départ, et 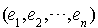 comme base de E espace d'arrivée. Cela peut être schématisé de la manière suivante :
comme base de E espace d'arrivée. Cela peut être schématisé de la manière suivante :
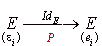
Alors on sait que (cliquez ici pour voir l'énoncé des propriétés utilisées) 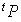 est la matrice de l'application identique de
est la matrice de l'application identique de 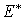 (qui est la transposée de l'application identique de E) en choisissant
(qui est la transposée de l'application identique de E) en choisissant 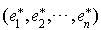 comme base de
comme base de 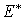 espace de départ et
espace de départ et 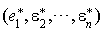 comme base de
comme base de 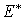 espace d'arrivée. Cela peut être schématisé de la manière suivante :
espace d'arrivée. Cela peut être schématisé de la manière suivante :
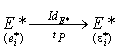
En remplaçant dans cette formule 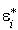 par
par 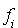 cela donne :
cela donne :
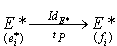
Donc  est la matrice de passage de la base
est la matrice de passage de la base 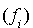 à la base
à la base 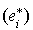 . Et par conséquent
. Et par conséquent 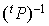 est la matrice de passage de la base
est la matrice de passage de la base 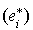 à la base
à la base 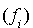 , soit R. Donc
, soit R. Donc 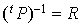 ce qui équivaut à
ce qui équivaut à 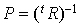 .
.
Le résultat obtenu est le suivant :
|
Propriété Soit Soit la base
Alors la matrice de passage P de la base
|
![]() Exemple :
Exemple :
Soit q l'application de 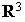 dans R définie pour tout
dans R définie pour tout 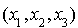 par
par 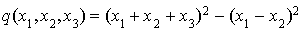
C'est bien une forme quadratique sur 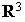 (expression polynômiale homogène de degré 2 par rapport aux
(expression polynômiale homogène de degré 2 par rapport aux 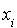 ). Cherchons une base orthogonale pour q.
). Cherchons une base orthogonale pour q.
On observe que 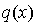 est une combinaison linéaire de carrés des formes linéaires
est une combinaison linéaire de carrés des formes linéaires 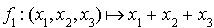 et
et 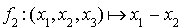 .
.
Il est clair que ces deux formes sont linéairement indépendantes. Donc on a une décomposition en combinaison linéaire de carrés de formes linéaires indépendantes. On en déduit immédiatement que q est de rang 2 (donc q est dégénérée).
D'après ce qui précède la première étape consiste à compléter la famille libre 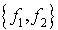 par une forme linéaire
par une forme linéaire 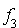 de manière à ce que
de manière à ce que 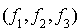 soit une base de
soit une base de 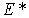 . Prenons par exemple
. Prenons par exemple 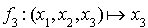 qui convient.
qui convient.
Pour trouver une base orthogonale, on va utiliser successivement les deux méthodes qui viennent d'être décrites.
Première méthode :
Soit 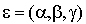 un vecteur de
un vecteur de 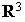 . C'est la base canonique qui joue le rôle de la base
. C'est la base canonique qui joue le rôle de la base 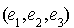 . Soit
. Soit 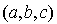 un élément de
un élément de 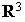 .
.
Première étape : résolution du système linéaire 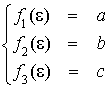
Avec les données numériques de l'exemple cela donne : 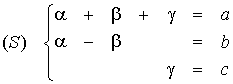 .
.
Il est équivalent au système : 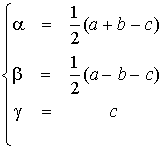
Deuxième étape : détermination des vecteurs 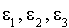 .
.
Cela revient à résoudre le système  successivement avec
successivement avec 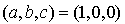 , puis
, puis 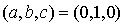 , et enfin
, et enfin 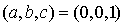 .
.
Vecteur 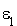 : on a :
: on a : 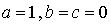 . Alors, d'après le résultat précédent :
. Alors, d'après le résultat précédent :
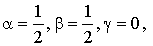 et donc
et donc 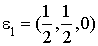 .
.
Vecteur 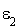 : on a :
: on a : 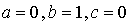 . Alors, d'après le résultat précédent :
. Alors, d'après le résultat précédent :
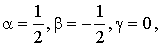 et donc
et donc 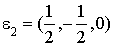 .
.
Vecteur 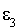 : on a :
: on a : 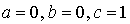 . Alors, d'après le résultat précédent :
. Alors, d'après le résultat précédent :
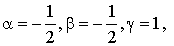 et donc
et donc 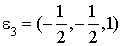 .
.
Deuxième méthode :
En conservant les notations précédentes, il vient 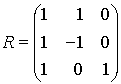 et donc
et donc 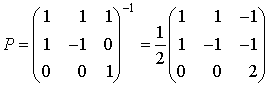 .
.
Cela donne la base orthogonale 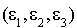 avec
avec 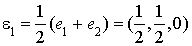 ,
, 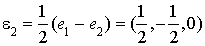 et
et 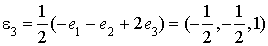 .
.
Il s'agit d'un algorithme permettant de trouver une décomposition d'une forme quadratique en combinaison linéaire de carrés de formes linéaires indépendantes.
Les identités suivantes sont les outils essentiels de cet algorithme :
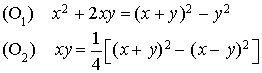
La preuve est basée sur une démonstration par récurrence sur la dimension n de E.
Si 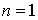 , il n'y a rien à dire.
, il n'y a rien à dire.
Supposons que toute forme quadratique sur un espace de dimension 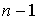 admette une décomposition en combinaison linéaire de carrés de formes linéaires indépendantes.
admette une décomposition en combinaison linéaire de carrés de formes linéaires indépendantes.
Soit q une forme quadratique sur un espace de dimension n.
Si 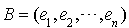 est une base quelconque de E, un élément x de E s'écrit
est une base quelconque de E, un élément x de E s'écrit 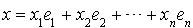 et
et 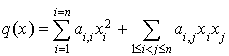 .
.
Premier cas : il existe au moins un indice i pour lequel 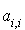 est non nul.
est non nul.
On dit usuellement qu'il existe un « terme carré ».
Par exemple supposons 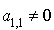 . Pour alléger l'écriture notons
. Pour alléger l'écriture notons 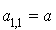 .
.
Alors 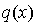 peut être ordonné comme un polynôme du second degré en
peut être ordonné comme un polynôme du second degré en 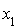 . Cela donne :
. Cela donne : 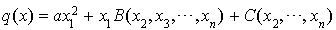 où B est une expression polynomiale homogène de degré 1 par rapport à
où B est une expression polynomiale homogène de degré 1 par rapport à 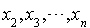 donc une forme linéaire en
donc une forme linéaire en 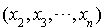 et C une expression polynomiale homogène de degré 2 par rapport à
et C une expression polynomiale homogène de degré 2 par rapport à 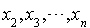 , donc une forme quadratique en
, donc une forme quadratique en 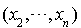 .
.
![]() Cliquez pour voir un rappel sur les formes linéaires
Cliquez pour voir un rappel sur les formes linéaires
En utilisant l'identité 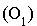 il vient :
il vient :
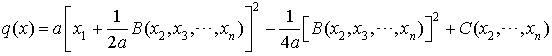
D'où 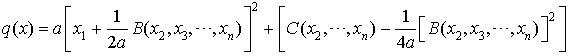 .
.
L'expression 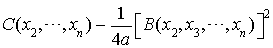 est une expression polynomiale homogène de degré 2 par rapport à
est une expression polynomiale homogène de degré 2 par rapport à 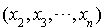 , qui peut donc être considérée comme une forme quadratique sur un espace de dimension
, qui peut donc être considérée comme une forme quadratique sur un espace de dimension 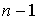 .
.
Cela permet d'écrire 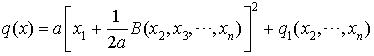 .
.
On termine en appliquant l'hypothèse de récurrence à 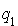 .
.
Second cas : il n'existe pas d'indice i pour lequel 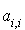 soit non nul.
soit non nul.
Si q est nulle c'est fini sinon il existe au moins un 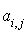 non nul (avec
non nul (avec 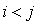 ). On dit usuellement que
). On dit usuellement que 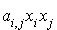 est un terme rectangle.
est un terme rectangle.
Par exemple supposons 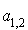 non nul et pour alléger l'écriture posons
non nul et pour alléger l'écriture posons 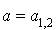 .
.
Alors 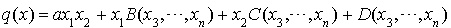 où B et C sont des formes linéaires en
où B et C sont des formes linéaires en 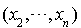 et D une forme quadratique en
et D une forme quadratique en 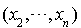 .
.
 | |
Voir une version animée de cette étape |
| Macromedia Flash - 45Ko | ||
Alors on peut écrire :
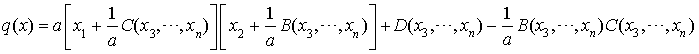
Autrement dit : 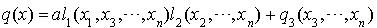 , où
, où 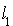 et
et 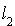 sont des formes linéaires en
sont des formes linéaires en 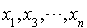 et
et 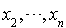 respectivement et
respectivement et 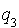 une forme quadratique en
une forme quadratique en 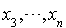 .
.
En utilisant l'identité (2), il vient :
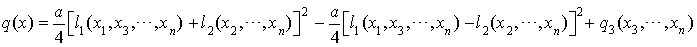
On peut appliquer l'hypothèse de récurrence à la forme quadratique 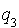 .
.
Dans les deux cas il est clair que les formes linéaires trouvées sont linéairement indépendantes, d'où le résultat.
Cela donne un algorithme pour trouver une décomposition de q en combinaison linéaire de carrés de formes linéaires linéairement indépendantes.
On commence en suivant la démarche précédente. Dans un cas comme dans l'autre, on aboutit soit à une expression de la forme 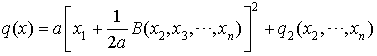 , soit à une expression de la forme :
, soit à une expression de la forme :
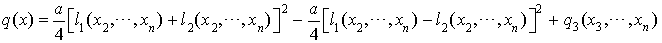
où 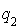 et
et 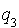 sont des formes quadratiques sur un espace de dimension strictement inférieur à n (ce sont des expressions polynomiales homogènes de degré 2 par rapport à
sont des formes quadratiques sur un espace de dimension strictement inférieur à n (ce sont des expressions polynomiales homogènes de degré 2 par rapport à 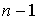 ou
ou 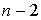 variables).
variables).
Pour continuer, on réitère le procédé pour 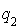 et
et 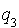 .
.
|
Remarque sur l'unicité et la méthode Il y a des choix arbitraires tout au long de l'algorithme. Par exemple, s'il y a plusieurs coefficients Par exemple on sait déjà, compte tenu du théorème d'existence, que le nombre de formes linéaires intervenant explicitement c'est-à-dire précédées d'un coefficient non nul se conserve puisque c'est le rang de la forme quadratique. |
|
Remarque sur la méthode Il y a bien sûr d'autres moyens d'écrire une forme quadratique comme combinaison linéaire de carrés de formes linéaires (voir l'exemple 2 suivant). La difficulté est de s'assurer que la méthode conduit à des formes linéaires, linéairement indépendantes. La méthode de Gauss assure cette indépendance linéaire qui n'a donc pas besoin d'être vérifiée à posteriori. |
![]() Exemple 1
Exemple 1
Soit q l'application de 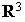 dans R définie pour tout
dans R définie pour tout 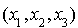 par :
par :
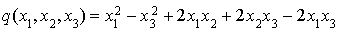
Première étape : il y a des termes « carrés » (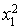 et
et 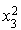 ).
).
On choisit 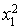 et on ordonne
et on ordonne 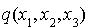 comme un polynôme en
comme un polynôme en 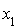 .
.
Cela donne : 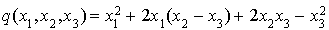 .
.
Deuxième étape : on utilise l'identité 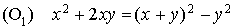 .
.
On obtient : 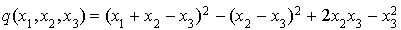
et par conséquent : 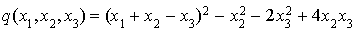 .
.
Troisième étape : on recommence pour la forme quadratique 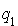 telle que
telle que 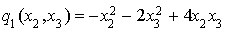 .
.
Il y a des termes carrés, on choisit par exemple 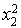 et cela donne :
et cela donne :
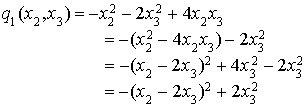
Donc 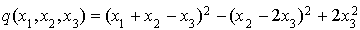 .
.
La forme quadratique q est donc de rang 3 (elle est par conséquent non dégénérée).
Cela permet de déterminer une base q-orthogonale 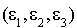 . En effet la matrice de passage de la base canonique à la base
. En effet la matrice de passage de la base canonique à la base 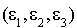 est :
est :
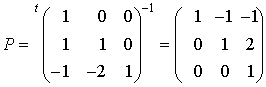 .
.
Donc 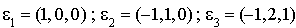 .
.
Si 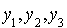 sont les coordonnées d'un vecteur x dans la base
sont les coordonnées d'un vecteur x dans la base 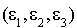 , alors on a
, alors on a 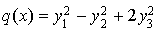 .
.
|
Remarque : Au niveau de la première étape on aurait pu choisir Ce calcul illustre le fait qu'il n'y a pas unicité. Remarquons qu'il y a trois formes linéaires affectées d'un coefficient non nul. Cela est normal puisque le nombre de formes est égal au rang de la forme quadratique considérée. Donc ici, toutes les décompositions de q en carrés feront intervenir 3 formes linéaires. |
![]() Exemple 2
Exemple 2
Soit q l'application de 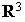 dans R définie pour tout
dans R définie pour tout 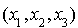 par :
par : 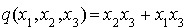 . C'est une forme quadratique.
. C'est une forme quadratique.
|
Remarque : En appliquant l'identité
L'expression trouvée est une combinaison linéaire de carrés de formes linéaires mais elles ne sont pas indépendantes. En effet soient les formes linéaires Alors Il était clair, à priori, que cette décomposition ne pouvait pas convenir car elle faisait intervenir quatre formes linéaires ; or q, forme quadratique sur |
On va utiliser la méthode de Gauss.
Première étape : il n'y a pas de termes « carrés ». On choisit donc un terme rectangle par exemple 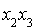 . On écrit
. On écrit 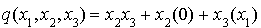 et on transforme cette expression de la façon suivante :
et on transforme cette expression de la façon suivante : 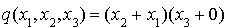 .
.
Deuxième étape : on applique l'identité 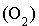 . Il vient alors :
. Il vient alors : 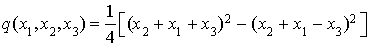 .
.
C'est terminé ; le rang de q est 2 et cela permet d'obtenir une base orthogonale dans laquelle la matrice associée à q est 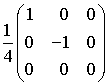 .
.
Une forme quadratique peut se décomposer de plusieurs façons en combinaison linéaire de carrés de formes linéaires indépendantes. On a déjà vu qu'il y a un invariant, à savoir le nombre de formes qui interviennent affectées d'un coefficient non nul puisque ce nombre est le rang de la forme quadratique. Cependant lorsque l'espace vectoriel considéré est un espace vectoriel réel, il y en a d'autres. Leur étude est l'objet de ce paragraphe.
Dans tout ce paragraphe, on considère un espace vectoriel sur le corps des nombres réels.
On a le théorème suivant :
|
Théorème : Théorème d'inertie de Sylvester Soit E un R-espace vectoriel de dimension n et f une forme bilinéaire symétrique sur E.
|
![]() Pour visualiser le résultat, cliquez.
Pour visualiser le résultat, cliquez.
Preuve du théorème de Sylvester
La démonstration est faite dans le cas où f est non nulle, le résultat étant évident si f est nulle. On suppose aussi  et
et 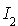 non vides, la démonstration des autres cas se faisant de la même façon. Pour la démonstration de la partie 2 du théorème, on supposera aussi que
non vides, la démonstration des autres cas se faisant de la même façon. Pour la démonstration de la partie 2 du théorème, on supposera aussi que 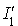 et
et 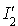 sont non vides.
sont non vides.
Rappelons tout d'abord ce que signifie l'hypothèse : les parties 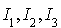 de
de 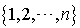 forment une partition de
forment une partition de 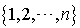 si et seulement si elles sont disjointes deux à deux et si
si et seulement si elles sont disjointes deux à deux et si 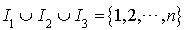 .
.
La première partie est une conséquence immédiate de l'existence d'une base orthogonale pour f. En effet si f est non nulle et si 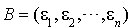 est une base orthogonale de E, on a, pour tout
est une base orthogonale de E, on a, pour tout 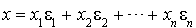 et
et 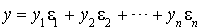 :
: 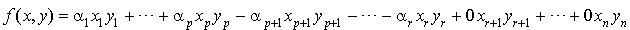
ou bien si 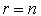 ,
, 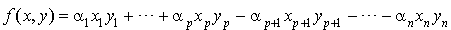
avec pour tout i, 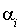 strictement positif.
strictement positif.
Alors en définissant 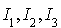 par
par 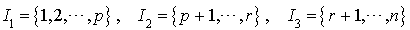 (
(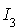 peut être vide) et la base
peut être vide) et la base 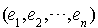 par :
par :
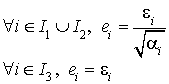
on a tous les éléments de la conclusion 1 du théorème et ils satisfont aux conditions voulues car :
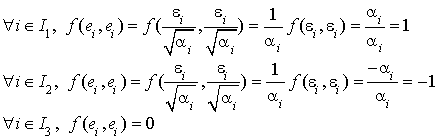
Deuxième partie :
On sait déjà que le nombre de coefficients non nuls est égal au rang de la forme bilinéaire symétrique. C'est le nombre d'éléments de 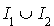 ou de
ou de 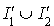 donc le nombre d'éléments de
donc le nombre d'éléments de 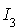 ou de
ou de 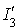 est le même (ne dépend que de f) et est égal à
est le même (ne dépend que de f) et est égal à 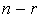 . On note p (respectivement
. On note p (respectivement 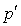 ) le nombre d'éléments de
) le nombre d'éléments de 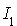 respectivement
respectivement 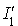 ), s (respectivement
), s (respectivement 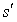 ) le nombre d'éléments de
) le nombre d'éléments de 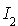 , (respectivement
, (respectivement 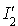 ) et
) et 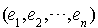 (respectivement
(respectivement 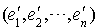 ) les bases de E satisfaisant aux conditions du (1).
) les bases de E satisfaisant aux conditions du (1).
Soit F le sous-espace vectoriel engendré par les vecteurs 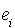 pour i appartenant à
pour i appartenant à 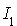 et
et 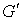 le sous-espace vectoriel engendré par les vecteurs
le sous-espace vectoriel engendré par les vecteurs 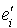 pour i appartenant à
pour i appartenant à 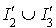 . Alors F est de dimension p et
. Alors F est de dimension p et 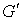 de dimension
de dimension 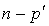 .
.
Montrons que 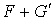 est une somme directe.
est une somme directe.
Soit x un élément de 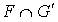 . Comme
. Comme 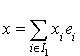 puisque x appartient à F,
puisque x appartient à F, 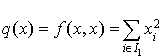 .
.
Comme 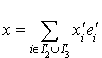 appartient à
appartient à 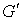 ,
, 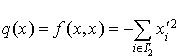 .
.
L'égalité 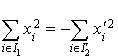 implique alors que :
implique alors que : 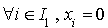 .
.
Donc 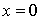 . On a donc démontré que
. On a donc démontré que 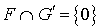 et donc que
et donc que 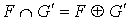 .
.
Comme 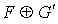 est un sous-espace vectoriel de E, sa dimension est inférieure ou égale à n et par conséquent on a l'inégalité :
est un sous-espace vectoriel de E, sa dimension est inférieure ou égale à n et par conséquent on a l'inégalité : 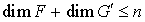
Donc 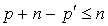 et par conséquent
et par conséquent 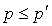 .
.
Le même raisonnement peut être fait en considérant 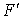 le sous-espace vectoriel engendré par les vecteurs
le sous-espace vectoriel engendré par les vecteurs 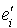 pour i appartenant à
pour i appartenant à 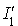 et G le sous-espace vectoriel engendré par les vecteurs
et G le sous-espace vectoriel engendré par les vecteurs 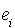 pour i appartenant à
pour i appartenant à 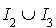 . Il conduit à l'inégalité
. Il conduit à l'inégalité 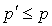 .
.
D'où 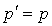 .
.
Comme 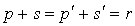 où r est le rang de la forme quadratique, on en déduit que
où r est le rang de la forme quadratique, on en déduit que 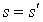 ce qui achève la démonstration.
ce qui achève la démonstration.
Le corollaire suivant, très utile dans la pratique, s'en déduit immédiatement.
|
Corollaire : Nombre de coefficients positifs et de coefficients négatifs dans une « décomposition en carrés » Soit q une forme quadratique sur un R -espace vectoriel de type fini.Quelle que soit la décomposition de q en combinaison linéaire de carrés de formes linéaires indépendantes, le nombre de coefficients strictement positifs est indépendant de la décomposition, de même que le nombre de coefficients strictement négatifs, et leur somme est égale au rang de la forme quadratique. |
La preuve en est immédiate. Si q est non nulle et de rang r et si l'on a une décomposition de q en carrés, quitte à changer l'ordre des coefficients, on peut l'écrire :
Si 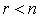
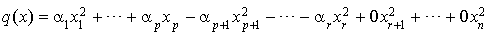
Si 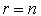
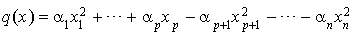
Alors, Si 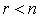 :
:
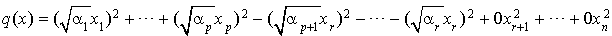 .
.
Si 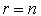 :
:
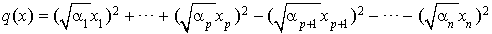 .
.
On est donc dans la situation du théorème et donc le nombre de signe +, de signe – et de termes nuls est constant.
On garde les notations et hypothèses du théorème de Sylvester. En particulier l'espace vectoriel considéré est un espace vectoriel sur R.
|
Définition : Signature d'une forme quadratique ou d'une forme bilinéaire symétrique La signature d'une forme quadratique q (ou d'une forme bilinéaire symétrique f) est le couple d'entiers |
On notera sgnq ou sgnf cette signature.
Cette définition a un sens puisque le théorème de Sylvester prouve que les deux entiers p et s et donc le couple 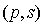 ne dépend que de la forme quadratique q et non pas de la décomposition.
ne dépend que de la forme quadratique q et non pas de la décomposition.
Avec les notations du théorème de Sylvester, p est le nombre d'éléments de 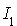 , s est celui de
, s est celui de 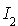 .
.
Ils vérifient l'égalité : 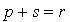 où r est le rang de la forme quadratique (ou de la forme bilinéaire symétrique).
où r est le rang de la forme quadratique (ou de la forme bilinéaire symétrique).
|
Propriétés Soit q une forme quadratique de signature
|
Preuve :
Ce résultat découle immédiatement du fait que 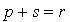 et qu'une forme quadratique est non dégénérée si et seulement si elle est de rang n.
et qu'une forme quadratique est non dégénérée si et seulement si elle est de rang n.
Si 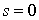 , la forme est positive (immédiat).
, la forme est positive (immédiat).
Si s est non nul, on peut écrire la forme quadratique sous la forme 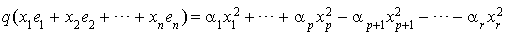 . où les
. où les 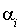 sont positifs ou nuls, avec au moins un
sont positifs ou nuls, avec au moins un 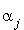 (
(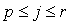 ) non nul. Alors
) non nul. Alors 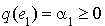 et
et 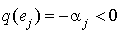 . Donc q n'est pas positive.
. Donc q n'est pas positive.
C'est une conséquence immédiate de 1. et 2. que l'on a mis en évidence car c'est un résultat très important.
Cela résulte immédiatement des définitions.
Vocabulaire : Une forme bilinéaire symétrique non dégénérée positive est aussi appelée forme bilinéaire symétrique définie positive.
Exemples
La forme quadratique q sur 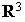 définie pour tout
définie pour tout 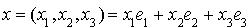 de
de 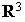 par :
par :
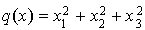 .
.
Sa signature est 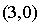 . Elle est donc non dégénérée positive.
. Elle est donc non dégénérée positive.
Soit q l'application de 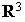 dans R définie pour tout
dans R définie pour tout 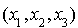 par :
par :
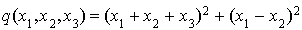 .
.
Elle est déjà décomposée en carrés et sa signature est 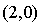 . Elle est donc positive et dégénérée. Il n'existe donc pas de base orthonormale relativement à q.
. Elle est donc positive et dégénérée. Il n'existe donc pas de base orthonormale relativement à q.
Soit q la forme quadratique sur 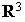 définie pour tout
définie pour tout 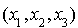 par :
par :
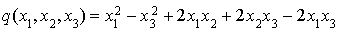 .
.
Grâce à la méthode de Gauss, on a trouvé :
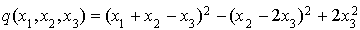 .
.
Alors la signature de q est 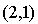 . Son rang est égal à 3 et elle est non dégénérée. Elle n'est pas positive. Il n'existe donc pas de base orthonormale relative à q.
. Son rang est égal à 3 et elle est non dégénérée. Elle n'est pas positive. Il n'existe donc pas de base orthonormale relative à q.
Soit 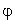 la forme quadratique sur
la forme quadratique sur 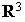 pour tout
pour tout 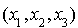 par :
par :
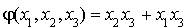 .
.
Grâce à la méthode de Gauss, on a trouvé :
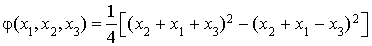 .
.
Alors la signature de 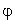 est
est 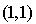 . Son rang est égal à 2, elle est dégénérée et n'est pas positive. Il n'existe donc pas de base orthonormale relativement à
. Son rang est égal à 2, elle est dégénérée et n'est pas positive. Il n'existe donc pas de base orthonormale relativement à 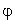 .
.
La propriété suivante concerne les formes bilinéaires symétriques positives.
|
Proposition : Inégalités de Cauchy-Schwarz Soit f une forme bilinéaire symétrique positive et q la forme quadratique associée. Alors :
|
La deuxième inégalité est aussi appelée inégalité de Minkowski.
Preuve :
1. Soient x et y deux éléments quelconques de E. Puisque la forme est positive, pour tout 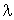 réel
réel 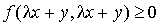 .
.
En développant cela donne : 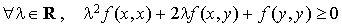 .
.
Ceci n'est possible que si le discriminant est négatif ou nul donc si 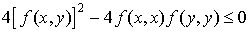 .
.
D'où la première formule.
Comme 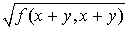 et
et 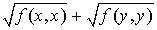 sont des réels positifs, l'inégalité
sont des réels positifs, l'inégalité 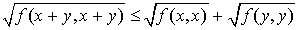 est équivalente à l'inégalité
est équivalente à l'inégalité 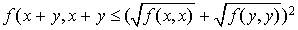 . Or :
. Or :
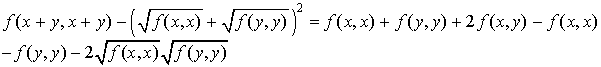
D'où 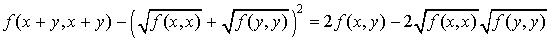
Or la quantité 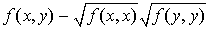 est négative ou nulle d'après la première inégalité. D'où le résultat.
est négative ou nulle d'après la première inégalité. D'où le résultat.
2. Soit 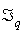 l'ensemble des vecteurs q-isotropes.
l'ensemble des vecteurs q-isotropes.
L'inclusion 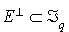 est toujours vraie. En effet, si x est un élément de
est toujours vraie. En effet, si x est un élément de 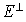 , il vient :
, il vient : 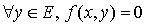 . En particulier si l'on prend
. En particulier si l'on prend 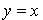 cela donne
cela donne 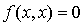 et donc x est isotrope.
et donc x est isotrope.
Supposons f positive. Soit x un vecteur isotrope. Alors en utilisant l'inégalité de Schwarz on obtient immédiatement la propriété : 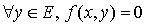 .
.
Pour terminer cette ressource donnons la définition suivante :
|
Définition : Espace euclidien Soit E un R-espace vectoriel de type fini et f une forme bilinéaire symétrique non dégénérée et positive. Le couple |
L'étude des espaces euclidiens fait l'objet d'une autre ressource.