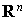 où n est un entier strictement positif. C'est un espace vectoriel sur R de dimension n. La base canonique joue au départ un rôle essentiel.
où n est un entier strictement positif. C'est un espace vectoriel sur R de dimension n. La base canonique joue au départ un rôle essentiel.
Il s'agit ici d'une ressource simple sur le sujet, destinée à un contexte où l'accent est mis sur les formes quadratiques et non pas sur les formes bilinéaires symétriques même si le vocabulaire et les liaisons existant entre ces deux notions sont données en fin de ressource. Le lien entre forme quadratique et matrice symétrique est essentiel dans cette ressource.
L'espace vectoriel considéré est Rn.
Prérequis indispensables :
Le vocabulaire de base de l'algèbre linéaire et la notion d'espace de type fini (ou dimension finie).
Le calcul matriciel et les formules de changement de base.
Objectifs :
Reconnaître une forme quadratique sur Rn.
Savoir écrire la matrice associée à une forme quadratique dans une base.
Savoir écrire la forme polaire d'une forme quadratique.
Temps de travail prévu : 60 minutes
Sommaire :
Il s'agit ici d'une ressource simple sur le sujet, destinée à un contexte où le l'accent est mis sur les formes quadratiques et non pas sur les formes bilinéaires symétriques, même si cette notion est introduite dans la dernière partie de cette ressource.
L'espace vectoriel considéré est 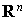 où n est un entier strictement positif. C'est un espace vectoriel sur R de dimension n. La base canonique joue au départ un rôle essentiel.
où n est un entier strictement positif. C'est un espace vectoriel sur R de dimension n. La base canonique joue au départ un rôle essentiel.
Les résultats qui vont être démontrés peuvent être prouvés de la même façon pour un espace vectoriel de dimension n.
L'espace vectoriel considéré est l'espace vectoriel 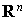 , espace vectoriel de dimension n.
, espace vectoriel de dimension n.
Un élément x de 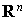 s'écrit
s'écrit 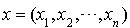 soit encore
soit encore  où
où  est la base canonique.
est la base canonique.
|
Définition : forme quadratique sur On appelle forme quadratique sur
|
L'application q est caractérisée par les réels 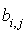 .
.
La définition suivante fixe le vocabulaire.
|
Définition : une expression polynômiale homogène de degré 2 par rapport aux Une expression de la forme |
Par conséquent une forme quadratique sur  est une application q de
est une application q de  dans R telle que si
dans R telle que si 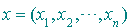 ,
, 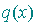 est une expression polynomiale homogène de degré 2 par rapport aux
est une expression polynomiale homogène de degré 2 par rapport aux  .
.
Exemple :
L'application q de  dans R définie pour tout
dans R définie pour tout  par
par 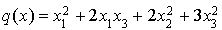 est une forme quadratique.
est une forme quadratique.
La propriété suivante justifie le vocabulaire et prouve qu'une forme quadratique non nulle n'est pas une application linéaire.
|
Proposition : Soit q une forme quadratique sur Soit x un élément quelconque de E et
|
Preuve :
Soit x un élément quelconque de 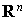 et
et 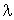 un réel quelconque.
un réel quelconque.
Alors  ,
,
et donc 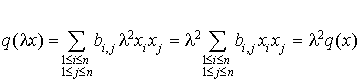 .
.
D'où le résultat.
Soit q une forme quadratique sur 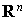 . Il existe donc
. Il existe donc 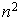 éléments de R,
éléments de R, 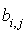 tels que
tels que
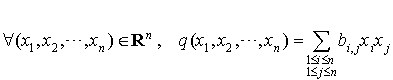
On peut réordonner les termes de cette expression en mettant en évidence les termes « carrés » c'est-à-dire de la forme  et les termes « rectangles » c'est-à-dire de la forme
et les termes « rectangles » c'est-à-dire de la forme 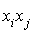 avec
avec 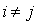 . Le coefficient du terme
. Le coefficient du terme  est
est 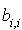 ; celui du terme
; celui du terme 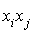 est
est 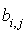 , et celui de
, et celui de 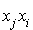 est
est 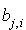 . Bien évidemment ces deux derniers termes peuvent être regroupés ce qui permet d'écrire :
. Bien évidemment ces deux derniers termes peuvent être regroupés ce qui permet d'écrire :
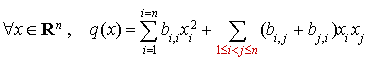
On introduit les scalaires  définis pour tout couple
définis pour tout couple 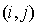 appartenant à
appartenant à 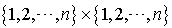 par :
par :
 .
.
Ils vérifient en particulier les relations :
 |
Alors :
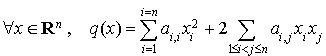
Sur l'exemple 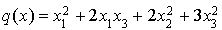 on a
on a 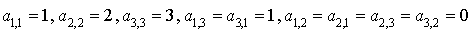 .
.
Dans toute la suite c'est cette expression d'une forme quadratique qui sera utilisée, à cause de la symétrie des coefficients c'est-à-dire de la propriété : 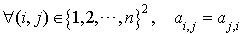 .
.
Il résulte de tout ce qui précède qu'une forme quadratique est entièrement caractérisée par les coefficients  , et donc par la matrice carrée d'ordre n dont le terme général est
, et donc par la matrice carrée d'ordre n dont le terme général est  . On peut donc énoncer la définition suivante :
. On peut donc énoncer la définition suivante :
|
Théorème-Définition : Matrice symétrique associée à une forme quadratique par rapport à une base Soit q une forme quadratique sur
On définit pour les couples
Alors la matrice A de terme général
On dit que c'est la matrice associée à q par rapport à la base canonique de |
L'introduction ici de la base canonique de  est due au double rôle tenu par les réels
est due au double rôle tenu par les réels  pour un n-uplet
pour un n-uplet 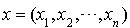 .
.
D'une part ce sont les composantes de x, et d'autre part ce sont les coordonnées de x dans la base canonique  puisque :
puisque :
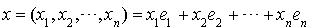
Exemple :
Reprenons l'exemple précédent. Soit q la forme quadratique définie pour tout  de
de  par
par 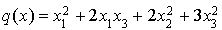 .
.
 | |
Voir une version animée de cette étape |
| Macromedia Flash - 31,8Ko | ||
La matrice qui lui est associée dans la base canonique est 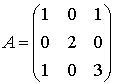 .
.
La réciproque est immédiate et on peut énoncer :
|
Théorème : Forme quadratique associée à une matrice symétrique Soit |
Cela conduit au théorème suivant :
|
Théorème : isomorphisme entre
L'espace vectoriel |
Démonstration :
La preuve du 1) est un simple calcul fait à partir de la définition, quant au 2) la bijection a été établie par les deux propositions précédentes et le fait que ce soit une application linéaire résulte aussi d'un simple calcul.
Soit  la base canonique de
la base canonique de 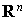 . Soit
. Soit 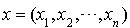 un élément de
un élément de 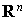 qui peut être écrit sur la base
qui peut être écrit sur la base  :
: 
Soit q la forme quadratique définie par :

Comme précédemment, on définit les scalaires  pour les couples
pour les couples 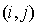 tels que
tels que  , par :
, par :
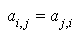
Alors, 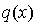 peut être écrit sous la forme :
peut être écrit sous la forme : 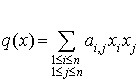
Soit A la matrice de 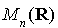 de terme général
de terme général  . C'est la matrice associée à q dans la base canonique.
. C'est la matrice associée à q dans la base canonique.
Soit  et
et  .
.
Alors, il vient :  .
.
En notant 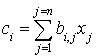 , cela donne
, cela donne 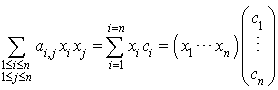 .
.
La matrice ligne  est égale à
est égale à 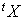 .
.
Le scalaire 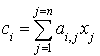 peut être interprété comme le produit
peut être interprété comme le produit  . Donc on a :
. Donc on a : 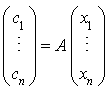 et au bilan
et au bilan  (bien sûr avec la convention d'identifier un matrice
(bien sûr avec la convention d'identifier un matrice  à un scalaire).
à un scalaire).
D'où la proposition :
|
Proposition : Ecriture matricielle de Soit q la forme quadratique sur
Si A est la matrice de |
La question qui se pose immédiatement est la suivante :
que se passe-t-il si au lieu de considérer la base canonique sur 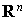 , on considère une autre base de
, on considère une autre base de 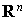 ?
?
Soient donc  la base canonique de
la base canonique de 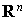 ,
,  une autre base de
une autre base de 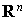 et P la matrice de passage de
et P la matrice de passage de  à
à 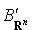 .
.
On peut écrire x sous la forme 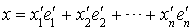 , et considérer la matrice colonne
, et considérer la matrice colonne 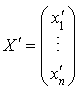 .
.
Les formules de changement de base donnent la relation 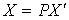 ; cela donne
; cela donne  , donc une expression de la forme
, donc une expression de la forme 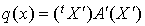 avec
avec 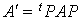 .
.
Si l'on développe ce produit de matrices, il est simple de voir que le résultat obtenu est :

où les 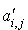 sont les coefficients de la matrice
sont les coefficients de la matrice  .
.
De plus 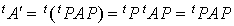 puisque A est symétrique. Donc la matrice
puisque A est symétrique. Donc la matrice  est symétrique.
est symétrique.
On en déduit deux résultats :
|
Proposition : Soit q une forme quadratique sur |
Cela permet aussi de définir la notion de matrice associée à une forme quadratique sur 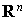 par rapport à n'importe quelle base de
par rapport à n'importe quelle base de 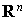 .
.
|
Proposition : matrice associée à une forme quadratique dans une base quelconque et formule de changement de base Si La matrice |
|
Remarque : Au départ la définition d'une forme quadratique sur C'est pourquoi tout ce qui vient d'être fait peut être généralisé à une espace vectoriel de type fini quelconque sur le corps des nombres réels ou sur le corps des nombres complexes. |
|
Définition : forme bilinéaire symétrique sur Une forme bilinéaire sur
Une forme bilinéaire est dite symétrique si :
|
Exemples :
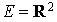 . Soit f l'application de
. Soit f l'application de 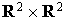 dans R définie par
dans R définie par  .
.
C'est une forme bilinéaire symétrique.
On peut remarquer que c'est le « produit scalaire euclidien » usuel utilisé dans la géométrie classique du plan.
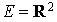 . Soit f l'application de
. Soit f l'application de 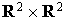 dans R définie par
dans R définie par  .
.
C'est une forme bilinéaire symétrique.
Soit 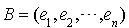 la base canonique de
la base canonique de 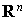 .
.
Soit f une forme bilinéaire symétrique sur 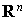 , x et y deux éléments de
, x et y deux éléments de 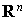 . On peut écrire
. On peut écrire 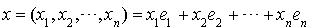 et
et 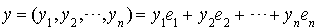 .
.
Alors :
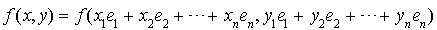
et donc :
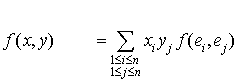
Pour aider à comprendre la construction de cette formule, on peut détailler ce calcul pour  . Cliquez ici pour voir ce calcul.
. Cliquez ici pour voir ce calcul.
La forme bilinéaire symétrique f est donc entièrement définie par les 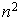 scalaires
scalaires 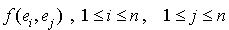 . Comme f est symétrique, il est immédiat que :
. Comme f est symétrique, il est immédiat que :
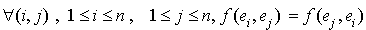
Réciproquement il est facile de vérifier que toute application de 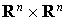 dans R de la forme
dans R de la forme 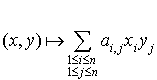 est une forme bilinéaire (les notations sont celles indiquées ci-dessus).
est une forme bilinéaire (les notations sont celles indiquées ci-dessus).
Cela permet donc d'énoncer la caractérisation, très utile dans la pratique :
|
Proposition : Caractérisation d'une forme bilinéaire sur Une application de
|
A partir d'une forme quadratique (ou d'une matrice symétrique) il est possible de construire une forme bilinéaire symétrique.
|
Théorème : forme bilinéaire symétrique associée à une forme quadratique ou à une matrice symétrique Soit E l'espace vectoriel
Alors :
|
Preuve :
Démonstration du 1 : elle est simple, il suffit de faire les calculs.
Démonstration du 2 :
Soit 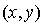 appartenant à
appartenant à 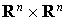 . Alors en utilisant la bilinéarité de f il vient :
. Alors en utilisant la bilinéarité de f il vient :
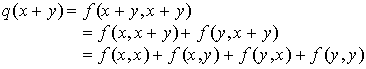
Comme f est symétrique cela donne :
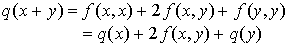
D'où le résultat.
Démonstration du 3 :
Il suffit d'appliquer la formule 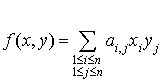 avec
avec  .
.
On a alors l'expression matricielle :
|
Proposition Les hypothèses et notations étant les mêmes que dans le théorème précédent, si x et y sont des éléments quelconques de |
La preuve de cette propriété résulte de la propriété 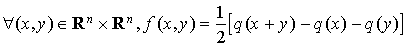 et de la formule
et de la formule 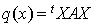 . Alors :
. Alors :

or, d'une part les matrices 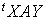 et
et 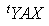 sont des matrices à une ligne une colonne donc égales à leur transposée, et d'autre part la matrice A est symétrique. Donc :
sont des matrices à une ligne une colonne donc égales à leur transposée, et d'autre part la matrice A est symétrique. Donc : 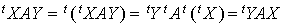 et par conséquent
et par conséquent 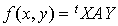 .
.
Exemple : géométrie euclidienne classique
Soit 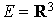 et
et  sa base canonique.
sa base canonique.
Soit l'application q de  dans R définie pour tout
dans R définie pour tout 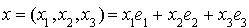 de
de  par :
par :
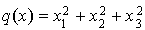 .
.
C'est une forme quadratique sur  .
.
Alors la matrice associée à q dans la base canonique est la matrice unité d'ordre 3 et la forme bilinéaire symétrique qui lui est associée (théorème précédent) est définie pour tout élément 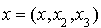 et
et 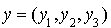 par :
par :
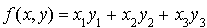 .
.
On reconnaît le produit scalaire euclidien de la géométrie classique, la quantité 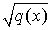 étant la norme euclidienne du vecteur x.
étant la norme euclidienne du vecteur x.
Une relation globale entre forme quadratique et forme bilinéaire symétrique est précisée dans le théorème suivant.
|
Théorème : Isomorphisme entre Soient
C'est donc un isomorphisme entre |
Les vérifications sont immédiates.
![]() Conséquence pratique :
Conséquence pratique :
Cela donne un procédé pratique pour déterminer explicitement la forme polaire d'une forme quadratique définie par :
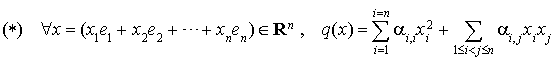
Notons 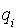 et
et 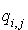 les formes quadratiques
les formes quadratiques 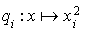 et
et 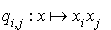 . La propriété
. La propriété  équivaut à :
équivaut à :
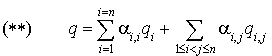
la propriété 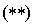 prouve que les formes
prouve que les formes 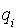 et
et 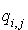 forment une famille génératrice de
forment une famille génératrice de 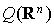 . Il est immédiat de vérifier qu'elles sont linéairement indépendantes. Elles définissent donc une base de
. Il est immédiat de vérifier qu'elles sont linéairement indépendantes. Elles définissent donc une base de 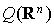 .
.
Cette base est extrêmement utile pour déterminer simplement la forme polaire associée à une forme quadratique donnée (dans l'autre sens si on connaît la forme bilinéaire symétrique, trouver la forme quadratique associée est immédiat, il suffit d'écrire  ).
).
En effet, à cause de l'isomorphisme indiqué dans le théorème, si f est la forme polaire associée à q, 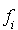 celle associée à
celle associée à 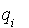 et si
et si 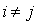 ,
, 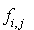 celle associée à
celle associée à 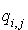 , il vient :
, il vient :
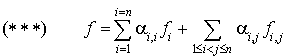
et les formes bilinéaires symétriques 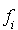 et
et 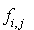 définissent une base de
définissent une base de 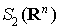 . Il ne reste donc qu'à les déterminer.
. Il ne reste donc qu'à les déterminer.
En utilisant la définition, il vient :
 et
et 
D'où la proposition :
|
Proposition : base de Les éléments de
et
Ces formes bilinéaires symétriques |
Ce qui donne le corollaire pratique suivant :
|
Corollaire : Expression explicite de la forme polaire d'une forme quadratique Si q est une forme quadratique sur
|
Ce résultat est constamment utilisé dans la pratique.
Exemple :
Soit 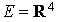 .
.
Soit q l'application de E dans R définie pour tout  par
par 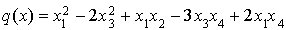
 | |
Voir une version animée de ces étapes |
| Macromedia Flash - 67,0Ko | ||
Comme 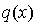 est une expression polynômiale homogène de degré 2 par rapport aux coordonnées
est une expression polynômiale homogène de degré 2 par rapport aux coordonnées 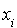 de x dans la base canonique, c'est une forme quadratique et sa forme polaire est définie pour tout
de x dans la base canonique, c'est une forme quadratique et sa forme polaire est définie pour tout  et
et 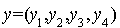 de
de 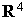 par
par  .
.
La matrice associée à f (ou à q) dans la base canonique de  est :
est :
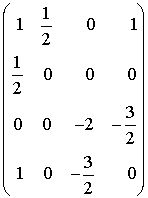 .
.