| 1 |
|
|
Signal "gaussien" pair de durée 2T
|
|
1 |
|
|
|
|
|
C'est un exemple traditionnel et facile à évaluer,
car :
 | il a une variation temporelle de type 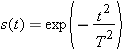 , |  | la largeur du signal est liée au paramètre 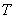 , |  | la transformée de Fourier d'un signal gaussien est également
gaussienne, |  |
ce signal est une bonne modélisation de fonctions de réponse
des appareils de mesures qu'on trouve en physique.
|
La représentation du signal  Signal "gaussien" pair de durée 2T
Pour le moment on va essentiellement s'attacher à la
gaussienne car :
 | elle va permettre de mettre en évidence une propriété de la
transformée de Fourier , |  | analytiquement, elle permet de calculer facilement ces
transformées de Fourier. |
|  |  |  |
Le spectre  La représentation du spectre |  |  |  |
Le lien entre les deux gaussiennes
Temporellement, on a vu que la gaussienne temporelle avait
une largeur qu'on peut évaluer à  et le spectre de cette
gaussienne dans le domaine
fréquentiel a une largeur qui à 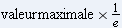 il faudra 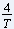 .
Ceci veut dire que plus 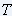 est petit, plus 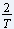 sera grand, en
d'autres termes, plus un événement temporel est bref, plus son spectre est
étendu.
|  |  |  |
 | Télécommunication
Dans le domaine des télécommunications, le but sera
d'envoyer un grand nombre d'informations par unité de temps, et donc plus un
événement temporel sera bref, plus son spectre sera large, il faut alors
disposer d'une largeur spectrale importante.
Ceci est l'un des éléments qui poussent à passer des radios
AM aux radios FM ou des transmissions GSM aux transmissions optiques.
|  |  |  |
|
|
|
| 3 |
3 |
3 |