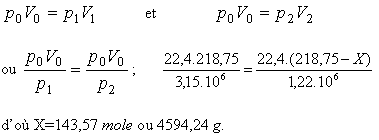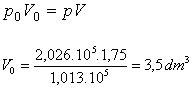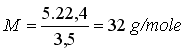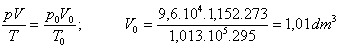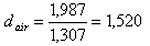| 1 |
|
|
Calcul du changement de l?état des gaz parfaits
|
|
1 |
|
|
|
|
|
Calcul du changement de l'état des gaz parfaits
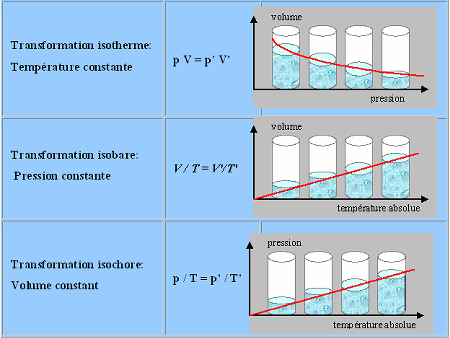
Les
trois lois permettent de calculer le changement de l'état des gaz lors de
différentes transformations.
 | Question
posée: Un ballon en acier contient 7 kg d'oxygène O2 sous une
pression de 3,55.10
Pa. Une partie de l'oxygène
était utilisée et la pression a diminuée jusqu'au 1,22.106 Pa.
Quelle est la masse de l'oxygène utilisé ?
Résolution:
Le nombre de moles dans 7 kg d'oxygène est 7000/32 =218,75 mole
Le volume du gaz
aux conditions normales (à PTN) est V1 = 22,4.218,75 dm3 = 4900 dm3.
Si le nombre de
moles de l'oxygène utilisé est X, dans le ballon restent (218,75-X) moles avec
un volume V2 à PTN
égal à 22,4. (218,75-X) dm3.
Comme le volume du
ballon est constant (V1 =
V2), par la loi de Boyle-Mariotte on a:
|  |  |  |
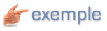 | Question
posée: Cinq grammes d'un gaz avec une masse molaire inconnue, à une température de 0°C et pression de 2,026.105 Pa
occupe un volume de
1,75 dm3. Calculer la
masse molaire du gaz.
Résolution:Le problème peut
être résolu de deux façons.
a/ La
masse molaire M peut être calculée à partir de la masse m d'un échantillon de
gaz dans des conditions de température et de pression données en utilisant
l'équation caractéristique des gaz parfaits.
b/ Suite de la loi
de Boyle-Mariotte, à T=const, m=const, si on connaît la pression et le volume occupé par un gaz
l'on peut calculer la pression ou le volume si l'autre paramètre est changé.
M g (1 mole à
PTN) occupent un volume de 22,4 dm3
5 g occupent un
volume de 3,5 dm3
|  |  |  |
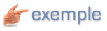 | Question
posée:
Un ballon en verre
contenant un gaz inconnu a une masse de 124,995 g. La masse du même ballon contenant de l'air est de 124,315 g.
Calculer la masse molaire du gaz si le volume du ballon est de 1,152 dm3, la température est de 22°C et la pression 9,6.104 Pa.
La masse molaire
moyenne de l'air est de 29 g/mole.
Résolution: Le volume du gaz à PTN peut être déterminé par
l'équation
A PTN, 1 mole de
l'air (29 g) occupe un volume de 22,4
dm3. La masse de 1,01 dm3 de l'air est 1,307 g.
La masse du ballon
est 124,315-1,307=123,008 g.
La masse du gaz
inconnu est donc 124,995-123,008=1,987 g.
La densité relative du
gaz inconnu par rapport de l'air est:
et sa masse molaire M = 29.1,52 = 44 g/mole - probablement CO2.
|  |  |  |
|
|
|
| 3 |
3 |
3 |