 .
.
Cette ressource contient quatre exercices guidés.
Le premier illustre la simplification qu'entraîne le théorème de Cayley-Hamilton dans le calcul de polynômes de matrices.
Dans le deuxième on recherche le polynôme minimal d'une matrice à paramètre.
Dans le troisième on calcule une puissance nième de matrice.
Dans le quatrième il s'agit de construire une matrice vérifiant une relation.
Prérequis indispensables :
Le calcul matriciel.
La théorie générale de la diagonalisation.
La division euclidienne des polynômes.
Le théorème de Cayley-Hamilton.
Le théorème sur les facteurs irréductibles du polynôme caractéristique et du polynôme minimal.
Le théorème : puissance d'une matrice et polynôme annulateur.
Objectifs :
Trouver le polynôme minimal à partir du polynôme caractéristique et réciproquement.
Calculer une puissance de matrice en utilisant un polynôme annulateur bien choisi.
Temps de travail prévu : 70 minutes
Sommaire :
Enoncé
Soit la matrice, à coefficients réels, 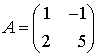 .
.
Déterminer le polynôme caractéristique de A.
En utilisant la division euclidienne du polynôme 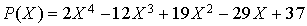 par le polynôme caractéristique de A, montrer qu'il existe des réels
par le polynôme caractéristique de A, montrer qu'il existe des réels 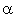 et
et 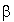 tels que la matrice
tels que la matrice 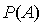 soit égale à la matrice
soit égale à la matrice 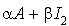 (préciser les valeurs de
(préciser les valeurs de 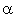 et
et 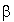 ).
).
En déduire que la matrice 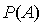 est inversible et écrire son inverse sous la forme
est inversible et écrire son inverse sous la forme 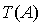 , avec
, avec 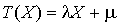 (
(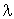 et
et 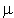 étant des réels à calculer).
étant des réels à calculer).
Durée : 20 minutes
Aide de lecture
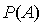 désigne la matrice
désigne la matrice 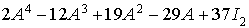 ,
,
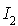 étant la matrice unité d'ordre 2.
étant la matrice unité d'ordre 2.
Aide de méthodologie
2. Effectuer la division euclidienne  puis en déduire
puis en déduire  .
.
3. Calculer le déterminant de  .
.
Effectuer puis simplifier le produit 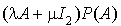 où
où 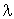 et
et 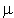 sont des réels quelconques, enfin choisir convenablement
sont des réels quelconques, enfin choisir convenablement 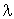 et
et 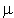 .
.
Aide supplémentaire
1. 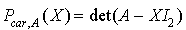 .
.
2. Rappel du théorème de Cayley-Hamilton : 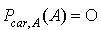 .
.
3. Une matrice est inversible si et seulement si son déterminant n'est pas nul.
Utiliser l'expression 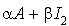 de
de 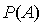 .
.
Exprimer 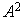 comme combinaison linéaire de A et
comme combinaison linéaire de A et 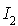 puis choisir
puis choisir 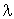 et
et 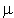 pour que
pour que 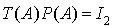 .
.
Solution
1. 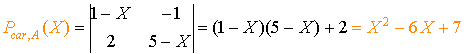 .
.
2. On effectue la division euclidienne demandée :
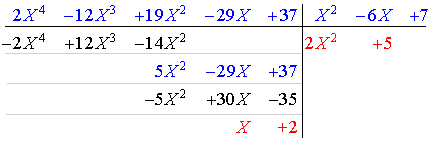
Ainsi 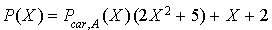 .
.
Alors 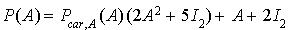 , or d'après le théorème de Cayley-Hamilton
, or d'après le théorème de Cayley-Hamilton 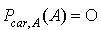 , d'où
, d'où 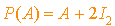 .
.
Les réels 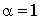 et
et 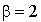 conviennent donc.
conviennent donc.
3. Pour étudier l'inversibilité de la matrice 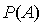 , on calcule son déterminant :
, on calcule son déterminant :
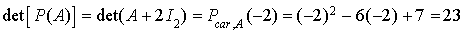
Donc ce déterminant n'est pas nul et la matrice 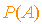 est inversible.
est inversible.
On cherche l'inverse de 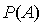 sous la forme
sous la forme 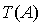 , avec
, avec 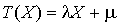 .
.
Soit deux réels 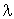 et
et 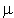 , si
, si 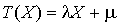 alors
alors 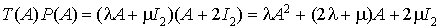 , mais d'après le théorème de Cayley-Hamilton
, mais d'après le théorème de Cayley-Hamilton 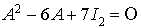 donc
donc 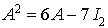 .
.
Ainsi 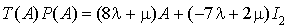 .
.
Pour trouver l'inverse de 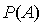 il suffit de résoudre le système suivant :
il suffit de résoudre le système suivant :
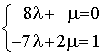 . Ce système a une unique solution
. Ce système a une unique solution 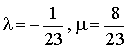 .
.
L'inverse de la matrice 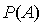 est donc la matrice
est donc la matrice 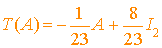 .
.
![]() Autre démonstration
Autre démonstration
On peut atteindre le résultat plus rapidement en utilisant la division euclidienne du polynôme caractéristique par 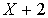 , reste de la division du polynôme P par le polynôme caractéristique.
, reste de la division du polynôme P par le polynôme caractéristique.
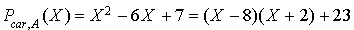
D'où 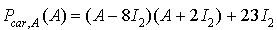 . En utilisant le théorème de Cayley-Hamilton et le résultat de la question précédente on obtient
. En utilisant le théorème de Cayley-Hamilton et le résultat de la question précédente on obtient 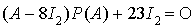 et enfin
et enfin 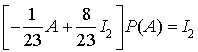 .
.
Enoncé
Déterminer, suivant les valeurs du paramètre réel m, le polynôme minimal de la matrice :
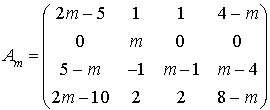
Durée : 20 minutes
Aide de méthodologie
Calculer le polynôme caractéristique, trouver la forme de ses diviseurs unitaires ayant les mêmes facteurs irréductibles puis rechercher, parmi eux, le polynôme annulateur de plus bas degré.
Aide supplémentaire
Distinguer les deux cas 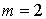 et
et 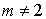 .
.
Solution
Le polynôme minimal étant un diviseur du polynôme caractéristique, on commence par calculer ce dernier :
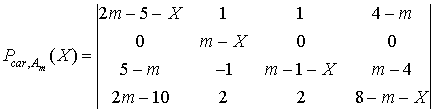
En développant suivant la ligne 2,
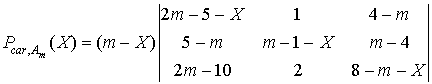
En effectuant les transformations 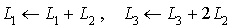 , puis en factorisant dans la ligne 1 et dans la ligne 3 :
, puis en factorisant dans la ligne 1 et dans la ligne 3 :
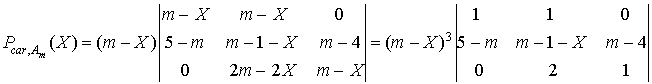
La transformation 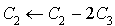 entraîne :
entraîne :
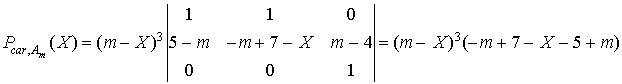
Donc 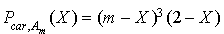 .
.
Suivant les valeurs de m, la matrice possède une ou deux valeurs propres.
![]() Etude du cas
Etude du cas 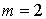
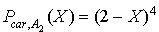 et
et 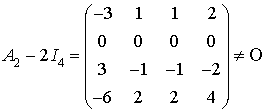
donc 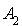 n'est pas diagonalisable et
n'est pas diagonalisable et 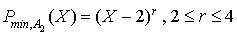 .
.
On calcule alors 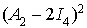 et on trouve la matrice nulle donc
et on trouve la matrice nulle donc 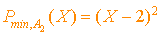 .
.
![]() Etude du cas
Etude du cas 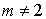
Dans ce cas la matrice possède une valeur propre simple et une valeur propre triple, donc son polynôme minimal est de la forme 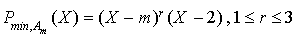 .
.
De plus c'est le polynôme annulateur de plus bas degré, on calcule alors 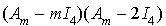 .
.
C'est à dire 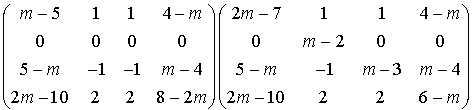 .
.
On remarque que les lignes de la matrice de gauche sont proportionnelles, il suffit donc de calculer le produit de la première par chacune des colonnes de celle de droite pour obtenir le produit matriciel.
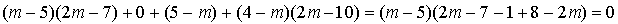
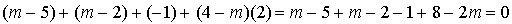
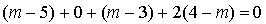
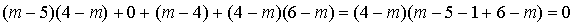
Tous ces produits étant nuls, 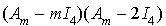 est la matrice nulle. Donc
est la matrice nulle. Donc 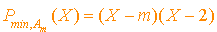 .
.
Remarque :
Dans ce cas le polynôme minimal est scindé et n'a que des racines simples d'où la matrice 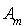 est diagonalisable.
est diagonalisable.
Enoncé
Soit la matrice 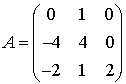 .
.
Calculer le polynôme caractéristique de A puis son polynôme minimal.
En déduire, pour tout entier strictement positif n, la matrice 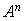 en fonction de A et de
en fonction de A et de 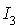 .
.
Durée : 15 minutes
Aide de méthodologie
2. Ecrire l'identité de la division euclidienne du polynôme 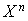 par le polynôme minimal en explicitant le reste
par le polynôme minimal en explicitant le reste 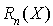 . En déduire que
. En déduire que 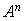 est égale à
est égale à 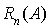 . Trouver les coefficients de
. Trouver les coefficients de 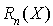 en utilisant la(es) racine(s) du polynôme minimal et leur(s) ordre(s) de multiplicité.
en utilisant la(es) racine(s) du polynôme minimal et leur(s) ordre(s) de multiplicité.
Aide supplémentaire
2. L'identité de la division euclidienne s'écrit :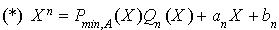
On en déduit par dérivation :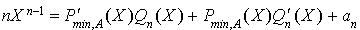
Solution
1. 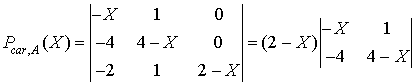 .
.
D'où 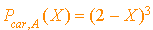 .
.
La matrice A possède une unique valeur propre et n'est pas diagonale donc elle n'est pas diagonalisable et son polynôme minimal est de la forme 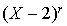 avec
avec 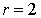 ou
ou 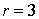 .
.
On calcule les puissances successives :
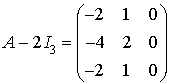 , puis
, puis 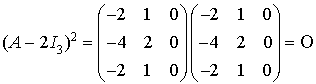 .
.
D'où 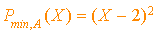 .
.
2. Soit n un entier strictement positif, la division euclidienne du polynôme 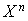 par le polynôme
par le polynôme 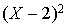 , de degré 2, s'écrit :
, de degré 2, s'écrit :
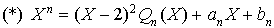
où 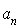 et
et 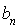 sont des nombres réels et
sont des nombres réels et 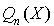 est un polynôme à coefficients réels.
est un polynôme à coefficients réels.
On en déduit 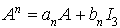 .
.
On recherche donc les réels 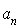 et
et 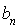 .
.
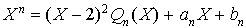 donc
donc 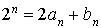 .
.
Une relation ne suffit pas pour trouver deux nombres. Le réel 2 étant racine double du polynôme 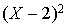 , on dérive la relation
, on dérive la relation 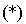 ainsi :
ainsi :
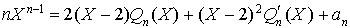
donc 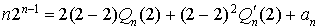
Ce qui entraîne 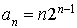 et
et 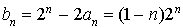 .
.
On conclut alors :
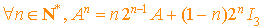
Enoncé
Soit A une matrice carrée d'ordre n à coefficients dans K, K étant R ou C, vérifiant la relation :
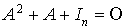
où 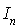 désigne la matrice unité d'ordre n.
désigne la matrice unité d'ordre n.
On suppose 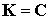 , montrer que la matrice A est diagonalisable.
, montrer que la matrice A est diagonalisable.
On suppose 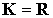 .
.
Montrer que la matrice A n'est pas diagonalisable.
Montrer que n est un entier pair.
On suppose 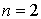 . Construire une telle matrice.
. Construire une telle matrice.
Trouver, à l'aide de la question précédente et pour tout entier n pair, une matrice réelle A d'ordre n vérifiant la relation 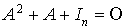 .
.
Durée : 15 minutes
Aide de méthodologie
2.b A partir du polynôme minimal, prévoir la forme du polynôme caractéristique.
2.c Ecrire A sous la forme 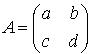 , et utiliser le lien entre le polynôme minimal et le polynôme caractéristique de cette matrice, pour choisir des réels a, b, c et d convenables.
, et utiliser le lien entre le polynôme minimal et le polynôme caractéristique de cette matrice, pour choisir des réels a, b, c et d convenables.
Aide supplémentaire
2.d Penser aux matrices par blocs.
Solution
1. Le polynôme 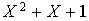 est un polynôme annulateur de A.
est un polynôme annulateur de A.
Dans 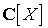 ce polynôme est égal à
ce polynôme est égal à 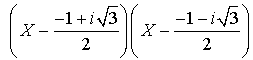 , il est donc scindé et n'a que des racines simples. Il en est de même de tout diviseur de ce polynôme et en particulier du polynôme minimal
, il est donc scindé et n'a que des racines simples. Il en est de même de tout diviseur de ce polynôme et en particulier du polynôme minimal  de A.
de A.
Par conséquent, la matrice A est diagonalisable.
Remarque : la matrice
A est inversible car 0 n'est pas une valeur propre de A (puisque 0 n'est pas racine du polynôme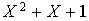 multiple de
multiple de 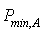 ).
).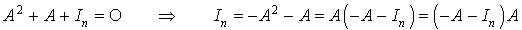 ,
, 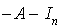 ).
).
2.a Dans 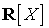 , le polynôme
, le polynôme 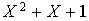 est un polynôme annulateur de A. Il est irréductible, c'est donc le polynôme unitaire de plus bas degré annulateur de A, et par conséquent
est un polynôme annulateur de A. Il est irréductible, c'est donc le polynôme unitaire de plus bas degré annulateur de A, et par conséquent 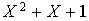 est le polynôme minimal de A.
est le polynôme minimal de A.
Ce polynôme n'étant pas scindé, la matrice A n'est pas diagonalisable.
De même que précédemment, la matrice A est inversible.
2.b De plus le polynôme minimal et le polynôme caractéristique de A ont les mêmes facteurs irréductibles. Donc le polynôme caractéristique de A est de la forme 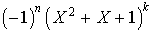 où k est un entier, d'où
où k est un entier, d'où 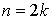 et n est pair.
et n est pair.
2.c Si 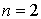 , d'après la question b), le polynôme caractéristique de A est
, d'après la question b), le polynôme caractéristique de A est 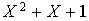 .
.
On cherche A sous la forme 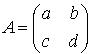 , où a, b, c et d sont des réels tels que
, où a, b, c et d sont des réels tels que 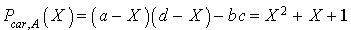 .
.
Donc il faut et il suffit que les réels a, b, c et d vérifient les équations 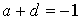 et
et 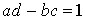 .
.
Par exemple les réels 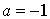 ,
, 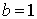 ,
, 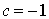 et
et 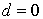 conviennent :
conviennent :
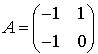
2.d On sait que si A est une matrice carrée d'ordre n, qui se présente comme un tableau diagonal de matrices carrées :
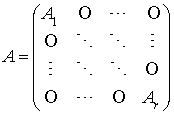 ,
,
alors 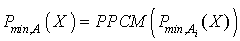 .
.
Donc, pour tout entier 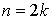 , il suffit de construire une matrice carrée d'ordre 2k se présentant comme un tableau diagonal de k matrices carrées d'ordre 2, ayant chacune le même polynôme minimal
, il suffit de construire une matrice carrée d'ordre 2k se présentant comme un tableau diagonal de k matrices carrées d'ordre 2, ayant chacune le même polynôme minimal 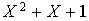 .
.
Par exemple, la matrice A de la forme indiquée précédemment avec 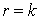 et
et 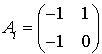 , pour tout i,
, pour tout i, 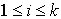 , vérifie bien
, vérifie bien 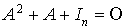 .
.