Deux éléments x et y de E tels que 
sont dits orthogonaux relativement à f (ou orthogonaux pour f, ou orthogonaux relativement à q, ou orthogonaux pour q, ou f-orthogonaux, ou q-orthogonaux).
Soit A une partie non vide de E. L'ensemble des vecteurs de E qui sont orthogonaux à tous les vecteurs de A pour f est appelé l'orthogonal de A pour f et est noté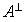 
: 
.
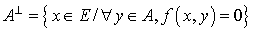Soient A et B deux parties non vides de E :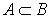 
.
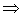
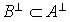Si A est non vide, 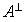est un sous-espace vectoriel de E.
L'orthogonal de A est égal à l'orthogonal du sous-espace vectoriel engendré par A :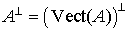 
.
L'orthogonal d'un sous-espace vectoriel F engendré par une famille finie de vecteurs de E est égal à l'orthogonal de cette famille.
.
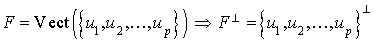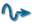
On appelle noyau de f (ou de q) l'orthogonal relativement à f de l'espace vectoriel E :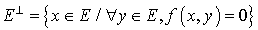 
.
La forme bilinéaire symétrique f (ou la forme quadratique q) est dite non dégénérée si le noyau de f (ou de q) est réduit au vecteur nul :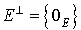
.
Si E est de type fini, M la matrice associée à f dans une base B et X le vecteur colonne dont les éléments sont les coordonnées dans B du vecteur x de E, alors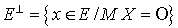 
.
La forme bilinéaire symétrique f est non dégénérée si et seulement si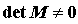 
.
Si E est de type fini,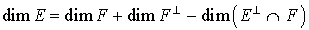 
Un vecteur x de E est isotrope pour f (ou q) s'il est orthogonal à lui même pour f, ce qui s'écrit 
L'ensemble des vecteurs isotropes pour f (ou q) s'appelle le cône isotrope de f (ou q).
Le sous-espace F est non isotrope pour f si le vecteur nul est le seul vecteur de F orthogonal à F, c'est à dire si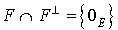 
.
Le sous-espace F est non isotrope pour f si et seulement si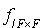 
est non dégénérée.
Si F est un sous-espace vectoriel de E de type fini, le sous-espace F est non isotrope pour f si et seulement si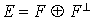 
.
Tableau récapitulatif quand E est de type fini :
|
Si M est la matrice associée à f dans une base B et X le vecteur colonne des coordonnées dans B du vecteur x de E, alors Si F est un sous-espace vectoriel de E, on a l'égalité |
|
|
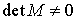
et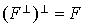 
.